
【题目】如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相较于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你认为正确结论的序号都填上).
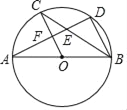
【答案】①③
【解析】
①由直径所对圆周角是直角,
②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
③由平行线得到∠OCB=∠DBC,再由圆的性质得到结论判断出∠OBC=∠DBC;
④得不到△CEF和△BED中对应相等的边,所以不一定全等.
解:①、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,
③、∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
④、∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故答案为:①③


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形是正方形,![]() ,
,![]() 垂直
垂直![]() ,点
,点![]() 、
、![]() 、
、![]() 在一条直线上,且
在一条直线上,且![]() 与
与![]() 恰好关于所在直线成轴对称.已知
恰好关于所在直线成轴对称.已知![]() ,正方形边长为
,正方形边长为![]() .
.
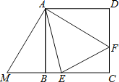
![]() 图中
图中![]() 可以绕点________按________时针方向旋转________后能够与
可以绕点________按________时针方向旋转________后能够与![]() ________重合;
________重合;
![]() 写出图中所有形状、大小都相等的三角形________;
写出图中所有形状、大小都相等的三角形________;
![]() 用
用![]() 、
、![]() 的代数式表示
的代数式表示![]() 与
与![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )
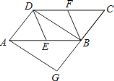
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是( )
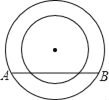
A. 4<AB<5 B. 6<AB<10 C. 6≤AB<10 D. 6<AB≤10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
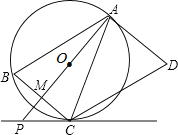
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
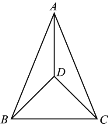
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,D、E分别是半径OA、OB的中点,C是![]() 上一点,CD=CE.
上一点,CD=CE.
(1)求证:![]() =
=![]() ;
;
(2)若∠AOB=120°,CD=![]() ,求半径OA的长.
,求半径OA的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com