
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
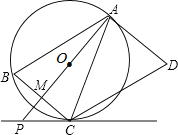
(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
【答案】(1)直线PC与圆O相切(2)![]()
【解析】解:(1)直线PC与圆O相切。理由如下::
如图,连接CO并延长,交圆O于点N,连接BN,
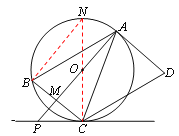
∵AB//CD,∴BAC=ACD。
∵BAC=BNC,∴BNC=ACD。
∵BCP=ACD,∴BNC=BCP。
∵CN是圆O的直径,∴CBN=90。
∴BNCBCN=90,∴BCPBCN=90。
∴PCO=90,即PCOC。
又∵点C在圆O上,∴直线PC与圆O相切。
(2)∵AD是圆O的切线,∴ADOA,即OAD=90。
∵BC//AD,∴OMC=180OAD=90,即OMBC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,AMC=90,AC=AB=9,MC=![]() BC=3,
BC=3,
由勾股定理,得![]() 。
。
设圆O的半径为r,
在Rt△OMC中,OMC=90,OM=AMAO=![]() ,MC=3,OC=r,
,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即![]() 。解得
。解得![]() 。
。
在△OMC和△OCP中,∵OMC=OCP,MOC=COP,∴△OMC~△OCP。
∴![]() ,即
,即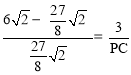 。∴
。∴![]() 。
。
(1)过C点作直径CE,连接EB,由CE为直径得∠E+∠BCE=90°,由AD∥BC得∠ACD=∠BAC,而
∠BAC=∠E,∠BCP=∠ACD,所以∠E=∠BCP,于是∠BCP+∠BCE=90°,然后根据切线的判断得到结论。
(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM=![]() BC=3,根据线段垂直平分线的性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=
BC=3,根据线段垂直平分线的性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM= ![]() 。设⊙O的半径为r,则OC=r,OM=AM-r=
。设⊙O的半径为r,则OC=r,OM=AM-r=![]() ,在Rt△OCM中,根据勾股定理计算出
,在Rt△OCM中,根据勾股定理计算出![]() ,从而由△OMC~△OCP得相似比可计算出PC。
,从而由△OMC~△OCP得相似比可计算出PC。


科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() ,
,![]() 两种商品,购买
两种商品,购买![]() 个
个![]() 商品比购买
商品比购买![]() 个
个![]() 商品多花
商品多花![]() 元,并且花费
元,并且花费![]() 元购买
元购买![]() 商品和花费
商品和花费![]() 元购买
元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元?
商品各需要多少元?
(2)若商店准备购买![]() ,
,![]() 两种商品共
两种商品共![]() 个,并且购买
个,并且购买![]() ,
,![]() 两种商品的总费用不超过
两种商品的总费用不超过![]() 元,那么商店至多购买
元,那么商店至多购买![]() 商品多少件?
商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相较于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你认为正确结论的序号都填上).
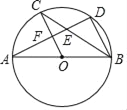
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=![]() x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM的最小值为________.
x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
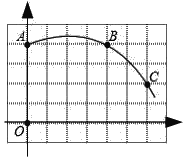
【题目】如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;.
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线交
的直线交![]() 轴负半轴于
轴负半轴于![]() ,且
,且![]() .
.

(1)求直线![]() 的函数表达式:
的函数表达式:
(2)如图2, ![]() 为
为![]() 轴上
轴上![]() 点右侧的一动点,以
点右侧的一动点,以![]() 为直角顶点,
为直角顶点,![]() 为一腰在第一象限内作等腰直角三角形
为一腰在第一象限内作等腰直角三角形![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() .当
.当![]() 点运动时,
点运动时,![]() 点的位置是否发生变化?如果不变请求出它的坐标:如果变化,请说明理由.
点的位置是否发生变化?如果不变请求出它的坐标:如果变化,请说明理由.
(3)直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,是否存在这样的直线
,是否存在这样的直线![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com