
【题目】如图,![]() ,
,![]() 、
、![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() 、
、![]() ,下列结论:
,下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
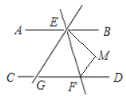
其中正确的是__________(填序号).
【答案】①②③.
【解析】
根据平行线的性质,即可判断①,由∠FEM=![]() ∠FEB,∠EFM=
∠FEB,∠EFM=![]() ∠EFD,∠FEB+∠EFD=180°,即可判断②,由
∠EFD,∠FEB+∠EFD=180°,即可判断②,由![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,得∠FEG=
,得∠FEG=![]() ∠AEF=
∠AEF=![]() ∠DFE=∠MFE,即可判断③,由
∠DFE=∠MFE,即可判断③,由![]() ,得∠BEG=∠EGC,若
,得∠BEG=∠EGC,若![]() ,则∠BEG=∠AEF,即:∠AEG=∠BEF,进而即可判断④.
,则∠BEG=∠AEF,即:∠AEG=∠BEF,进而即可判断④.
∵![]() ,
,
∴![]() ,
,
∴①正确,
∵![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,
,
∴∠FEM=![]() ∠FEB,∠EFM=
∠FEB,∠EFM=![]() ∠EFD,
∠EFD,
∵∠FEB+∠EFD=180°,
∴∠FEM+∠EFM=![]() ×180°=90°,
×180°=90°,
∴②正确,
∵![]() ,
,
∴∠AEF=∠DFE,
∵![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,
,
∴∠FEG=![]() ∠AEF=
∠AEF=![]() ∠DFE=∠MFE,
∠DFE=∠MFE,
∴![]() ,
,
∴③正确,
∵![]() ,
,
∴∠BEG=∠EGC,
若![]() ,则∠BEG=∠AEF,即:∠AEG=∠BEF,
,则∠BEG=∠AEF,即:∠AEG=∠BEF,
但∠AEG与∠BEF不一定相等,
∴④错误,
故答案是:①②③.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数 | 6 | 10 | 12 | |
棱数 | 9 | 12 | ||
面数 | 5 | 8 |
观察上表中的结果,你能发现![]() 、
、![]() 、
、![]() 之间有什么关系吗?请写出关系式
之间有什么关系吗?请写出关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
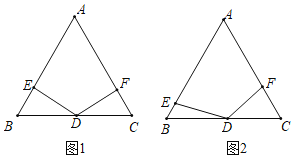
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
问题初探:
(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为______;
问题再探:
(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用
(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将进货单价40元的商品按50元出售,能卖出500个,已知这种商品每涨价1元,就会少销售10个。为了赚得8000元的利润,售价应定为多少?这时应进货多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在自动向西的公路l上有一检查站A,在观测点B的南偏西53°方向,检查站一工作人员家住在与观测点B的距离为7![]() km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈
km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈![]() ,cos76°≈
,cos76°≈![]() ,tan 76°≈4,sin53°≈
,tan 76°≈4,sin53°≈![]() ,tan53°≈
,tan53°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
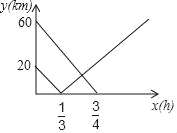
【题目】在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
(1)直接写出连接A、B两市公路的路程以及货车由B市到达A市所需时间.
(2)求机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式.
(3)求机场大巴与货车相遇地到机场C的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com