
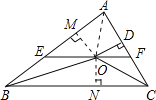
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )

A.①②③B.①②④C.②③④D.①③④
【答案】A
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF,故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF,故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=![]() mn,故④错误.
mn,故④错误.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣![]() ∠A,
∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
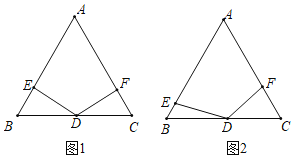
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
问题初探:
(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为______;
问题再探:
(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用
(3)若边长AB=4,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L的变化范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
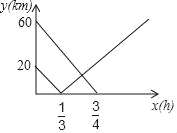
【题目】在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
(1)直接写出连接A、B两市公路的路程以及货车由B市到达A市所需时间.
(2)求机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式.
(3)求机场大巴与货车相遇地到机场C的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
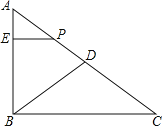
【题目】如图,在Rt△ABC中,∠ABC=90°,AC=15cm,BC=12cm,点D是线段AC的中点,动点P从A﹣D﹣B﹣C向终点C出发,速度为5cm/s,当点P不与点A、B重合时,作PE⊥AB交线段AB于点E,设点P的运动时间为t(s),△APE的面积为S(cm2).
(1)写出线段AB的长;
(2)当点P在线段BD上时,求PE的长(用含t的式子表示);
(3)当点P沿A﹣D﹣B运动时,用含t的代数式表示S;
(4)点E关于直线AP的对称点为E′,当点E′落在△ABC的内部时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人
捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均 每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
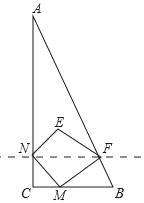
【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°.再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF.已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)用含t的代数式表示出NC与NF;
(2)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值,如果不能,说明理由;
(3)求y与t的函数关系式及相应t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]() ,
,
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_____________.
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底__________(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
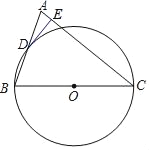
【题目】已知:如图,在△ABC中,AC=BC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)求证:DE是⊙O的切线;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com