
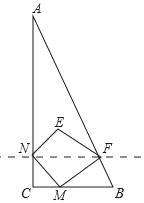
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABCÖŠ£¬”ĻC=90”ć£¬µćM“ÓµćC³ö·¢ŃŲCB·½ĻņŅŌ1cm/sµÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬µ½“ļµćBĶ£Ö¹ŌĖ¶Æ£¬ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬¹żµćM×÷Ö±ĻßMN½»ACÓŚµćN£¬ĒŅ±£³Ö”ĻNMC=45”ć£®ŌŁ¹żµćN×÷ACµÄ“¹Ļß½»ABÓŚµćF£¬Į¬½ÓMF£¬½«”÷MNF¹ŲÓŚÖ±ĻßNF¶Ō³ĘŗóµĆµ½”÷ENF£®ŅŃÖŖAC=8cm£¬BC=4cm£¬ÉčµćMŌĖ¶ÆŹ±¼äĪŖt£Øs£©£¬”÷ENFÓė”÷ANFÖŲµž²æ·ÖµÄĆ껿ĪŖy£Øcm2£©£®
£Ø1£©ÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾³öNCÓėNF£»
£Ø2£©ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ÄÜ·ńŹ¹µĆĖıߊĪMNEFĪŖÕż·½ŠĪ£æČē¹ūÄÜ£¬Ēó³öĻąÓ¦µÄtÖµ£¬Čē¹ū²»ÄÜ£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©ĒóyÓėtµÄŗÆŹż¹ŲĻµŹ½¼°ĻąÓ¦tµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©CN=t£¬NF=![]() £»£Ø2£©ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ÄÜŹ¹µĆĖıߊĪMNEFĪŖÕż·½ŠĪ£¬tµÄÖµĪŖ
£»£Ø2£©ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ÄÜŹ¹µĆĖıߊĪMNEFĪŖÕż·½ŠĪ£¬tµÄÖµĪŖ![]() £»£Ø3£©y=©
£»£Ø3£©y=©![]() t2+2t£Ø0£¼t”Ü2£©£»y=
t2+2t£Ø0£¼t”Ü2£©£»y=![]() £Ø8©t£©2£Ø2£¼t”Ü4£©£»£®
£Ø8©t£©2£Ø2£¼t”Ü4£©£»£®
”¾½āĪö”æ
£Ø1£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæÉÖŖ£ŗCN=CM=t£¬ĄūÓĆĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż¶ØĄķ
æÉµĆ£ŗ![]() £¬ÓÉ“Ė¼“æÉĒó³öNF£»
£¬ÓÉ“Ė¼“æÉĒó³öNF£»
£Ø2£©ÓÉŅŃÖŖµĆ³öCN=CM=t£¬FN”ĪBC£¬ÓɶŌ³ĘµÄŠŌÖŹµĆ³ö”ĻENF=”ĻMNF=”ĻNMC=45”ć£¬
MN=NE£¬OE=OM=CN=t£¬ÓÉÕż·½ŠĪµÄŠŌÖŹµĆ³ö![]() £¬µĆ³ö·½³Ģ£¬½ā·½³Ģ
£¬µĆ³ö·½³Ģ£¬½ā·½³Ģ
¼“æÉ£»
£Ø3£©·ÖĮ½ÖÖĒéæö£ŗ¢Łµ±0£¼t”Ü2Ź±£¬ÓÉČż½ĒŠĪĆ껿µĆ³ö![]()
¢Śµ±2£¼t”Ü4Ź±£¬×÷GH”ĶNFÓŚH£¬ÓÉ£Ø1£©µĆ£ŗ![]() GH=NH£¬GH=2FH£¬µĆ³ö
GH=NH£¬GH=2FH£¬µĆ³ö
![]() ÓÉČż½ĒŠĪĆ껿µĆ³ö
ÓÉČż½ĒŠĪĆ껿µĆ³ö![]()
½ā£ŗ£Ø1£©”ß”ĻC=90”ć£¬”ĻNMC=45”ć£¬
”ąCN=CM=t£¬
”ßAC=8£¬
”ąAN=8©t£¬
”ßNF”ĪBC£¬
”ą![]()
”ą![]()
”ą![]()
£Ø2£©ÄÜŹ¹µĆĖıߊĪMNEFĪŖÕż·½ŠĪ£»ĄķÓÉČēĻĀ£ŗ
Į¬½ÓME½»NFÓŚO£¬ČēĶ¼1ĖłŹ¾£ŗ
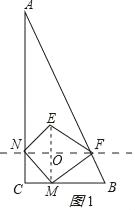
ÓɶŌ³ĘµÄŠŌÖŹµĆ£ŗ”ĻENF=”ĻMNF=”ĻNMC=45”ć£¬MN=NE£¬OE=OM=CN=t£¬
”ßĖıߊĪMNEFŹĒÕż·½ŠĪ£¬
”ą![]()
”ą![]()
½āµĆ£ŗ![]()
¼“ŌŚµćMµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ÄÜŹ¹µĆĖıߊĪMNEFĪŖÕż·½ŠĪ£¬tµÄÖµĪŖ![]() £»
£»
£Ø2£©·ÖĮ½ÖÖĒéæö£ŗ
¢Łµ±0£¼t”Ü2Ź±£¬ ![]()
¼“![]()
¢Śµ±2£¼t”Ü4Ź±£¬ČēĶ¼2ĖłŹ¾£ŗ×÷GH”ĶNFÓŚH£¬
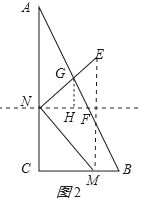
ÓÉ£Ø1£©µĆ£ŗ![]() GH=NH£¬GH=2FH£¬
GH=NH£¬GH=2FH£¬
”ą![]()
”ą![]()
¼“![]()



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=![]() £Ø
£Ø![]() £©£¬½«Ļ߶ĪBCČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪBD”£
£©£¬½«Ļ߶ĪBCČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪBD”£

£Ø1£©ČēĶ¼1£¬Ö±½ÓŠ“³ö”ĻABDµÄ“󊔣ØÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾£©£»
µÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©ČēĶ¼2£¬”ĻBCE=150”ć£¬”ĻABE=60”ć£¬ÅŠ¶Ļ”÷ABEµÄŠĪד²¢¼ÓŅŌÖ¤Ć÷£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½įDE£¬Čō”ĻDEC=45”ć£¬Ēó![]() µÄÖµ”£
µÄÖµ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]()

![]() Ēó³öÅ×ĪļĻß
Ēó³öÅ×ĪļĻß![]() µÄ¶Ō³ĘÖįŗĶ¶„µć×ų±ź£»
µÄ¶Ō³ĘÖįŗĶ¶„µć×ų±ź£»
![]() ŌŚÖ±½Ē×ų±źĻµÖŠ£¬Ö±½Ó»³öÅ×ĪļĻß
ŌŚÖ±½Ē×ų±źĻµÖŠ£¬Ö±½Ó»³öÅ×ĪļĻß![]() £Ø×¢Ņā£ŗ¹Ų¼üµćŅŖ×¼Č·£¬²»±ŲŠ“³ö»Ķ¼ĻóµÄ¹ż³Ģ£©£»
£Ø×¢Ņā£ŗ¹Ų¼üµćŅŖ×¼Č·£¬²»±ŲŠ“³ö»Ķ¼ĻóµÄ¹ż³Ģ£©£»
![]() øł¾ŻĶ¼Ļó»Ų“š£ŗ
øł¾ŻĶ¼Ļó»Ų“š£ŗ
¢Ł![]() Č”Ź²Ć“ÖµŹ±£¬Å×ĪļĻßŌŚ
Č”Ź²Ć“ÖµŹ±£¬Å×ĪļĻßŌŚ![]() ÖįµÄÉĻ·½£æ
ÖįµÄÉĻ·½£æ
¢Ś![]() Č”Ź²Ć“ÖµŹ±£¬
Č”Ź²Ć“ÖµŹ±£¬![]() µÄÖµĖę
µÄÖµĖę![]() µÄÖµµÄŌö“ó¶ų¼õŠ”£æ
µÄÖµµÄŌö“ó¶ų¼õŠ”£æ
![]() øł¾ŻĶ¼ĻóÖ±½ÓŠ“³ö²»µČŹ½
øł¾ŻĶ¼ĻóÖ±½ÓŠ“³ö²»µČŹ½![]() µÄ½ā¼Æ£®
µÄ½ā¼Æ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē½ńĶعżĪ¢ŠÅÅóÓŃȦ·¢²¼×Ō¼ŗĆæĢģŠŠ×ߵIJ½ŹżŅŃ³ÉĪŖŅ»ÖÖŹ±ÉŠ£®”°½”Éķ“ļČĖ”±Š”ÕÅĪŖĮĖĮĖ½āĖūµÄĪ¢ŠÅÅóÓŃȦĄļ“ó¼ŅµÄŌĖ¶ÆĒéæö£¬Ė껜³éČ”ĮĖ²æ·ÖŗĆÓŃ½ųŠŠµ÷²é£¬°ŃĖūĆĒ1ŌĀ29ČÕÄĒĢģĆæČĖŠŠ×ߵIJ½ŹżĒéæö·ÖĪŖĪåøöĄą±š£ŗA£Ø0”«4000²½£©£ØĖµĆ÷£ŗ0”«4000±ķŹ¾“óÓŚ»ņµČÓŚ0£¬Š”ÓŚ»ņµČÓŚ4000£¬ĻĀĶ¬£©”¢B£Ø4001”«8000²½£©”¢C£Ø8001”«12000²½£©”¢D£Ø12001”«16000²½£©”¢E£Ø16000²½ŅŌÉĻ£©£¬²¢½«Ķ³¼Ę½į¹ū»ęÖĘĮĖČēĶ¼1ŗĶ2Į½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®

ĒėÄćøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Š”ÕÅĖ껜³éČ”ĮĖ”” ””ĆūĪ¢ŠÅÅóÓŃȦŗĆÓŃ£»
£Ø2£©½«Ķ¼1µÄĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ŅŃÖŖŠ”ÕŵÄĪ¢ŠÅÅóÓŃȦĄļ¹²300ČĖ£¬Ēėøł¾Ż±¾“Ī³é²éµÄ½į¹ū£¬¹Ą¼ĘŌŚĖüµÄĪ¢ŠÅÅóÓŃȦĄļ1ŌĀ29ČÕÄĒĢģŠŠ×ß²»³¬¹ż8000²½µÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻABCŗĶ”ĻACBµÄĘ½·ÖĻßĻą½»ÓŚµćO£¬¹żµćO×÷EF”ĪBC½»ABÓŚE£¬½»ACÓŚF£¬¹żµćO×÷OD”ĶACÓŚD£¬ĻĀĮŠĖÄøö½įĀŪ£ŗ
¢ŁEF£½BE+CF£»
¢Ś”ĻBOC£½90”ć+![]() ”ĻA£»
”ĻA£»
¢ŪµćOµ½”÷ABCø÷±ßµÄ¾ąĄėĻąµČ£»
¢ÜÉčOD£½m£¬AE+AF£½n£¬ŌņS”÷AEF£½mn£®
ĘäÖŠÕżČ·µÄ½įĀŪŹĒ£Ø””””£©

A.¢Ł¢Ś¢ŪB.¢Ł¢Ś¢ÜC.¢Ś¢Ū¢ÜD.¢Ł¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£¬ĻĀĮŠĢõ¼ž²»ÄÜÅŠ¶ØĖıߊĪABCDĪŖĘ½ŠŠĖıߊĪµÄŹĒ£Ø””””£©
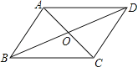
A.AB”ĪCD£¬AD”ĪBCB.OA£½OC£¬OB£½OD
C.AD£½BC£¬AB”ĪCDD.AB£½CD£¬AD£½BC
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖBD“¹Ö±Ę½·ÖAC£¬”ĻBCD=”ĻADF£¬AF”ĶAC£¬
£Ø1£©Ö¤Ć÷ABDFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōAF=DF=5£¬AD=6£¬ĒóACµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćA(m£¬6)£¬B(n£¬1)ŌŚ·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬AD”ĶxÖįÓŚµćD£¬BC”ĶxÖįÓŚµćC£¬µćEŌŚCDÉĻ£¬CD=5£¬”÷ABEµÄĆ껿ĪŖ10£¬ŌņµćEµÄ×ų±źŹĒ_____________£®
µÄĶ¼ĻóÉĻ£¬AD”ĶxÖįÓŚµćD£¬BC”ĶxÖįÓŚµćC£¬µćEŌŚCDÉĻ£¬CD=5£¬”÷ABEµÄĆ껿ĪŖ10£¬ŌņµćEµÄ×ų±źŹĒ_____________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚĢŻŠĪABCDÖŠ£¬AD”ĪBC£¬”ĻB=90”ć£¬AD=24cm£¬BC=26cm£¬¶ÆµćP“ÓµćA³ö·¢ŃŲAD·½ĻņĻņµćDŅŌ1cm/sµÄĖŁ¶ČŌĖ¶Æ£¬¶ÆµćQ“ÓµćCæŖŹ¼ŃŲ×ÅCB·½ĻņĻņµćBŅŌ3cm/sµÄĖŁ¶ČŌĖ¶Æ£®µćP”¢Q·Ö±š“ÓµćAŗĶµćCĶ¬Ź±³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļ¶ĖµćŹ±£¬ĮķŅ»µćĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®
£Ø1£©¾¹ż¶ą³¤Ź±¼ä£¬ĖıߊĪPQCDŹĒĘ½ŠŠĖıߊĪ£æ
£Ø2£©¾¹ż¶ą³¤Ź±¼ä£¬ĖıߊĪPQBAŹĒ¾ŲŠĪ£æ
£Ø3£©¾¹ż¶ą³¤Ź±¼ä£¬µ±PQ²»Ę½ŠŠÓŚCDŹ±£¬ÓŠPQ=CD£®

²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com