
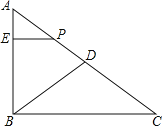
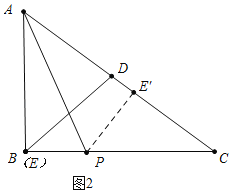
【题目】如图,在Rt△ABC中,∠ABC=90°,AC=15cm,BC=12cm,点D是线段AC的中点,动点P从A﹣D﹣B﹣C向终点C出发,速度为5cm/s,当点P不与点A、B重合时,作PE⊥AB交线段AB于点E,设点P的运动时间为t(s),△APE的面积为S(cm2).
(1)写出线段AB的长;
(2)当点P在线段BD上时,求PE的长(用含t的式子表示);
(3)当点P沿A﹣D﹣B运动时,用含t的代数式表示S;
(4)点E关于直线AP的对称点为E′,当点E′落在△ABC的内部时,直接写出t的取值范围.
【答案】(1)9;(2)12﹣4t;(3)S=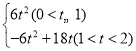 ;(4)
;(4)![]() <t<3或3<t<3.9
<t<3或3<t<3.9
【解析】
(1)在Rt△ABC中,根据勾股定理即可解决问题.
(2)只要证明△PBE∽△CAB,可得![]() ,由此即可解决问题.
,由此即可解决问题.
(3)分两种情形讨论①当0<t≤3时.②当3<t<6时,根据三角形的面积公式求出AE、PE即可解决问题.
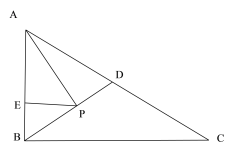
(4)求出两个特殊点的时间①如图1中,当点E关于AP的对称点E′在线段AC上时.如图2中,当点P在BC上,点E关于AP的对称点E′在线段AC上时.即可解决问题.
(1)∵在Rt△ABC中,∠ABC=90°,AC=15cm,BC=12cm,
∴AB=![]() ,
,
即AB的长为9;
(2)∵PE⊥AB,BC⊥AB,
∴PE∥BC,∠ABC=∠BEP=90°,
∴∠EPB=∠PBC,
∵点D为AC中点,
∴BD=CD=![]() AC,
AC,
∴∠DBC=∠DCB,
∴∠EPB=∠DCB,
∴△PBE∽△CAB,
∴![]()
∴![]() ,
,
∵BP=15﹣5t,
∴PE=12﹣4t.
(3)当0<t≤3时
AE=5t×![]() =3t,PE=5t×
=3t,PE=5t×![]() =4t,
=4t,
S=![]() PEAE=
PEAE=![]() 4t3t=6t2,
4t3t=6t2,
∴S=6t2.
当3<t<6时,
AE=9﹣(15﹣5t)×![]() =3t,PE=(15﹣5t)×
=3t,PE=(15﹣5t)×![]() =12﹣4t,
=12﹣4t,
S=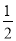 PEAE=
PEAE=![]() 3t(12﹣4t)=﹣6t2+18t.
3t(12﹣4t)=﹣6t2+18t.
∴S=﹣6t2+18t,
综上所述,S=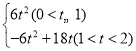 .
.
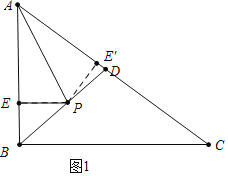
(4)如图1中,当点E关于AP的对称点E′在线段AC上时.作PE′⊥AC于E′,则PE=PE′
∵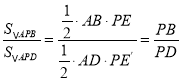 ,
,
∴![]() ,
,
∴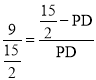 ,
,
∴PD=![]() ,
,
∴点P运动的时间=(![]() )÷5=
)÷5=![]() s,
s,
观察图象可知当![]() <t<3时,当点E′落在△ABC的内部.
<t<3时,当点E′落在△ABC的内部.
如图2中,当点P在BC上,点E关于AP的对称点E′在线段AC上时.
同理可得![]() ,
,
∴![]() ,
,
∴PB=4.5,
∴∴点P运动的时间=(![]() +4.5)÷5=3.9s
+4.5)÷5=3.9s
观察图象可知当3<t<3.9时,当点E′落在△ABC的内部.
综上所述,当![]() <t<3或3<t<3.9时,当点E′落在△ABC的内部.
<t<3或3<t<3.9时,当点E′落在△ABC的内部.


科目:初中数学 来源: 题型:
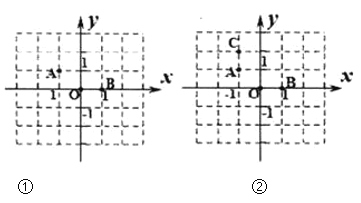
【题目】在棋盘中建立如图①所示的平面直角坐标系,二颗棋子![]() 、
、![]() 、
、![]() 的位置如图,它们的坐标分别为
的位置如图,它们的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)如图②,添加棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 为端点的四条首尾连接的线段围成的图形成为轴对称图形,请在图中画出该图形的对称轴;
为端点的四条首尾连接的线段围成的图形成为轴对称图形,请在图中画出该图形的对称轴;
(2)在其它格点位置添加一颗棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 为端点的首尾连接的四条线段构成一个轴对称图形,请直接写出点
为端点的首尾连接的四条线段构成一个轴对称图形,请直接写出点![]() 的坐标。(写山2个即可)
的坐标。(写山2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
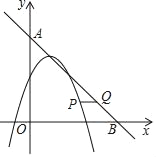
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()

![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今通过微信朋友圈发布自己每天行走的步数已成为一种时尚.“健身达人”小张为了了解他的微信朋友圈里大家的运动情况,随机抽取了部分好友进行调查,把他们1月29日那天每人行走的步数情况分为五个类别:A(0~4000步)(说明:0~4000表示大于或等于0,小于或等于4000,下同)、B(4001~8000步)、C(8001~12000步)、D(12001~16000步)、E(16000步以上),并将统计结果绘制了如图1和2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)小张随机抽取了 名微信朋友圈好友;
(2)将图1的条形统计图补充完整;
(3)已知小张的微信朋友圈里共300人,请根据本次抽查的结果,估计在它的微信朋友圈里1月29日那天行走不超过8000步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )

A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:

(1)根据图示求出表中的![]() 、
、![]() 、
、![]()
平均数 | 中位数 | 众数 | |
九(1) |
| 85 |
|
九(2) | 85 |
| 100 |
![]() ,
,![]() ,
,![]() .
.
(2)小明同学已经算出了九(2)班复赛成绩的方差:
![]() ,请你求出九(1)班复赛成绩的方差
,请你求出九(1)班复赛成绩的方差![]() ;
;
(3)根据(1)、(2)中计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com