
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
【答案】(1) 商家一次购买这种产品50件时,销售单价恰好为2600元;(2) 当0≤x≤10时,y=600x;当10<x≤50时,y =-10x2+700x;当x>50时,y =200x;(3) 公司应将最低销售单价调整为2750元.
【解析】
试题分析: (1)根据:原定售价-超过10件而降低的价格=实际售价,列方程可得;
(2)由销售单价均不低于2600元求出x的取值范围,根据实际售价不同分0≤x≤10、10<x≤50、x>50三种情况列出函数关系式;
(3)根据题意,此时情形满足10<x≤50时,y与x的函数关系,根据二次函数性质可求得最值并确定此时x的值.
试题解析:(1)设件数为x,根据题意,
得:3000-10(x-10)=2600,
解得:x=50,
答:商家一次购买这种产品50件时,销售单价恰好为2600元;
(2)由题意,得:3000-10(x-10)≥2600,
解得:x≤50,
当0≤x≤10时,y=(3000-2400)x=600x;
当10<x≤50时,y=[3000-2400-10(x-10)]x=-10x2+700x;
当x>50时,y=(2600-2400)x=200x;
(3)由y=-10x2+700x可知抛物线开口向下,
当x=-![]() =35时,利润y有最大值,
=35时,利润y有最大值,
此时销售单价为;3000-10×(35-10)=2750(元),
答:公司应将最低销售单价调整为2750元.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴相交于A,B两点,并与直线
与x轴相交于A,B两点,并与直线![]() 交于B,C两点,其中点C是直线
交于B,C两点,其中点C是直线![]() 与y轴的交点,连接AC.
与y轴的交点,连接AC.
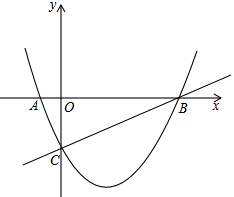
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马拉松赛选手分甲、乙两组运动员进行了艰苦的训练,他们在相同条件下各10次比赛,成绩的平均数相同,方差分别为0.25,0.21,则成绩较为稳定的是_________(选填“甲”或“乙)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据2010年第六次全国人口普查公布的数据显示,全桂林市总人口为498.84万人,那么用科学记数法表示为( )人.
A. 4.98846 B. 4.9884×106 C. 4.9884×107 D. 4.9884×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
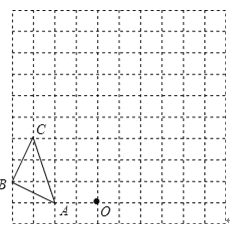
(1)把△ABC绕点O顺时针旋转90°得到△A1B1C1;
(2)以图中的O为位似中心,在△A1B1C1的同侧将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把a、b中较小的数记作min{a,b},设函数f (x)={![]() ,|x-2|}.若动直线y=m与函数y=f (x)的图象有三个交点,它们的横坐标分别为x1、x2、x3,则x1x2x3的最大值为_________
,|x-2|}.若动直线y=m与函数y=f (x)的图象有三个交点,它们的横坐标分别为x1、x2、x3,则x1x2x3的最大值为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我校一块边长为2x米的正方形空地是八年级1﹣4班的卫生区,学校把它分成大小不同的四块,采用抽签的方式安排卫生区,下图是四个班级所抽到的卫生区情况,其中1班的卫生区是一块边长为(x﹣2y)米的正方形,其中0<2y<x.
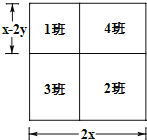
(1)分别用x、y的式子表示八年3班和八年4班的卫生区的面积;
(2)求2班的卫生区的面积比1班的卫生区的面积多多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com