
【题目】在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用![]() 元购进医用口罩若干个,第二次又用
元购进医用口罩若干个,第二次又用![]() 元购进该款口罩,但第二次每个口罩的进价是第一次进价的
元购进该款口罩,但第二次每个口罩的进价是第一次进价的![]() 倍,购进的数量比第一次少
倍,购进的数量比第一次少![]() 个.
个.
(1)求第一次和第二次分别购进的医用口罩数量为多少个?
(2)药店第一次购进口罩后,先以每个![]() 元的价格出售,卖出了
元的价格出售,卖出了![]() 个后购进第二批同款口罩,由于进价提高了,药店将口罩的售价也提升至每个
个后购进第二批同款口罩,由于进价提高了,药店将口罩的售价也提升至每个![]() 元继续销售卖出了
元继续销售卖出了![]() 个后,因当地医院医疗物资紧缺,将其已获得口罩销售收入
个后,因当地医院医疗物资紧缺,将其已获得口罩销售收入![]() 元和剩余全部的口罩捐赠给了医院.求药店捐赠口罩至少有多少个?
元和剩余全部的口罩捐赠给了医院.求药店捐赠口罩至少有多少个?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
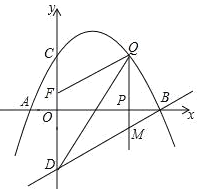
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P做
,0),过点P做![]() 轴的垂线l交抛物线于点Q,交直线BD于点M.
轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB运动过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),当点P在
),当点P在![]() 轴上运动时,试求
轴上运动时,试求![]() 为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
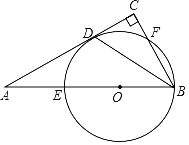
【题目】如图所示,Rt△ABC中:∠C=90°,AB=6,在AB上取点O,以O为圆心,以OB为半径作圆,与AC相切于点D,并分别与AB,BC相交于点E,F(异于点B).
(1)求证:BD平分∠ABC;
(2)若点E恰好是AO的中点,求弧BF的长;
(3)若CF的长为1,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ABC,
ABC,![]() A1B1C1,
A1B1C1,![]() A2B2C2,
A2B2C2,![]() A3B3C3…
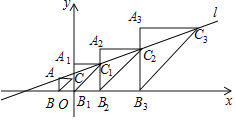
A3B3C3…![]() AnBnCn都是等腰直角三角形,点B,B1,B2,B3…Bn都在x轴上,点B1与原点重合,点A,C1,C2,C3…Cn都在直线l:y=
AnBnCn都是等腰直角三角形,点B,B1,B2,B3…Bn都在x轴上,点B1与原点重合,点A,C1,C2,C3…Cn都在直线l:y=![]() x+
x+![]() 上,点C在y轴上,AB∥A1B1∥A2B2∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥…∥AnCn∥x轴,若点A的横坐标为﹣1,则点Cn的纵坐标是_____.
上,点C在y轴上,AB∥A1B1∥A2B2∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥…∥AnCn∥x轴,若点A的横坐标为﹣1,则点Cn的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,![]() ,
,![]() ,
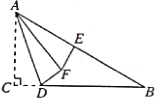
,![]() ,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC和正方形DEFG按如图所示摆放,其中 D,E两点分别在AB,BC上,且BD=DE.若AB=12,DE=4,则△EFC的面积为( )
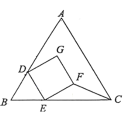
A.4B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出):有同样大小正方形256个,拼成如图1所示的![]() 的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?
的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?

(问题探究):我们先考虑以下简单的情况:一条直线穿越一个正方形的情况.(如图2)
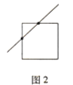
从图中我们可以看出,当一条直线穿过一个小正方形时,这条直线最多与正方形上、下、左、右四条边中的两个边相交,所以当一条直线穿过一个小正方形时,这条直线会与其中某两条边产生两个交点,并且以两个交点为顶点的线段会全部落在小正方形内.
这就启发我们:为了求出直线![]() 最多穿过多少个小正方形,我们可以转而去考虑当直线
最多穿过多少个小正方形,我们可以转而去考虑当直线![]() 穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
再让我们来考虑![]() 正方形的情况(如图3):
正方形的情况(如图3):
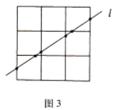
为了让直线穿越更多的小正方形,我们不妨假设直线![]() 右上方至左下方穿过一个
右上方至左下方穿过一个![]() 的正方形,我们从两个方向来分析直线
的正方形,我们从两个方向来分析直线![]() 穿过
穿过![]() 正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线
正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线![]() 最多可穿过
最多可穿过![]() 的大正方形中的六条线段,从而直线
的大正方形中的六条线段,从而直线![]() 上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线
上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线![]() 最多能经过5个小正方形.
最多能经过5个小正方形.
(问题解决):
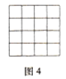
(1)有同样大小的小正方形16个,拼成如图4所示的![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
(2)有同样大小的小正方形256个,拼成![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
(3)如果用一条直线穿过![]() 的大正方形的话,最多可以穿过___________个小正方形.
的大正方形的话,最多可以穿过___________个小正方形.
(问题拓展):
(4)如果用一条直线穿过![]() 的大长方形的话(如图5),最多可以穿过个___________小正方形.
的大长方形的话(如图5),最多可以穿过个___________小正方形.
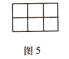
(5)如果用一条直线穿过![]() 的大长方形的话(如图6),最多可以穿过___________个小正方形.
的大长方形的话(如图6),最多可以穿过___________个小正方形.
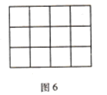
(6)如果用一条直线穿过![]() 的大长方形的话,最多可以穿过________个小正方形.
的大长方形的话,最多可以穿过________个小正方形.
(类比探究):
由二维的平面我们可以联想到三维的立体空间,平面中的正方形中四条边可联想到正方体中的正方形的六个面,类比上面问题解决的方法解决如下问题:
(7)如图7有同样大小的小正方体8个,拼成如图所示的![]() 的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
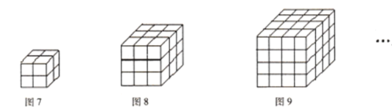
(8)如果用一条直线穿过![]() 的大正方体的话,最多可以穿过_________个小正方体.
的大正方体的话,最多可以穿过_________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
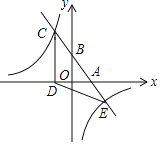
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com