
分析 利用多项式乘以多项式法则计算各式即可;
(1)根据上述规律写出结果即可;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的规律计算即可得到结果.
解答 解:(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1,
故答案为:x2-1;x3-1;x4-1;
(1)(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1;
(2)(x-1)(xn-1+xn-2+xn-3+…+x+1)=xn-1;
故答案为:(1)x7-1;(2)xn-1;
(3)1+2+22+23+24+…+235
=(2-1)(235+234+233+…+2+1)
=236-1.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
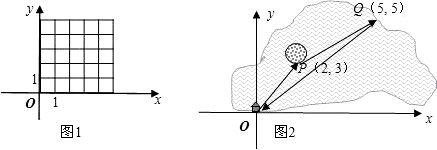
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解冰箱的使用寿命,采用普查的方式 | |
| B. | 为了了解全国中学生的视力状况,采用普查的方式 | |
| C. | 为了了解人们保护水资源的意识,采用抽样调查的方式 | |
| D. | 对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
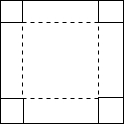 如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.
如图,在边长为acm的正方形纸片的四角处各剪去边长为xcm的正方形,然后沿虚线折叠成一个无盖的长方体盒子,则盒子的容积为a2x-4ax2+4x3cm3,当a=8cm,x=1.5cm时,盒子的容积为37.5cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
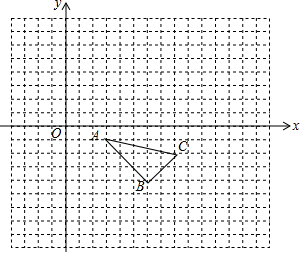 如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为(3,-1),(6,-4),(8,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com