【题目】如图，AO
OM，OA=4，点B为射线OM上的一个动点，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF.等腰Rt△ABE，连接EF交OM于P点，当点B在射线OM上移动时，则PB的长度为_________．
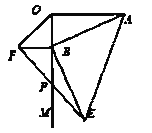
【答案】2.
【解析】试题分析：作辅助线，首先证明△ABO≌△BEN，得到BO=ME；进而证明△BPF≌△MPE，即可解决问题．如图，过点E作EN⊥BM，垂足为点N，∵∠AOB=∠ABE=∠BNE=90°，∴∠ABO+∠BAO=∠ABO+∠NBE=90°，∴∠BAO=∠NBE，∵△ABE、△BFO均为等腰直角三角形，∴AB=BE，BF=BO；在△ABO与△BEN中，∠BAO=∠NBE，∠AOB=∠BNE，AB=BE，∴△ABO≌△BEN（AAS），∴BO=NE，BN=AO；∵BO=BF，∴BF=NE，在△BPF与△NPE中，∠FBP=∠ENP，∠FPB=∠EPN，BF=NE，∴△BPF≌△NPE（AAS），∴BP=NP=
BN；而BN=AO，∴BP=AO=×4=2.
故答案为：2．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】(1)如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A(0，1)，B(1，0).在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=
.
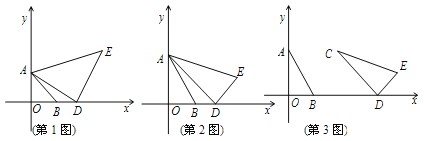
①求出E点的坐标(可用含m的代数式表示)；
②证明对于任意正数m，点E都在直线
上；
(2)将(1)中的两个等腰直角三角形都改为有一个角为
的直角三角形,如图22-2，A(0,
)，B(1，0). Rt△ADE中, ∠ADE=,∠AED=
. D（m,0）是x轴正半轴上任意一点,则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；
(3)将(2)中Rt△AOB保持不动,取点C(2, ),在x轴正半轴上取D（m,0）(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=，∠CED=.当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
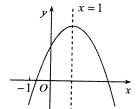
【题目】已知二次函数
的图象如图所示，有下列5个结论：① 
；② 
；③ 
；④ 
； ⑤ 
，（
的实数）其中正确的结论有
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】质量检查员准备从一批产品中抽取10件进行检查，如果是随机抽取，为了保证每件产品被检的机会均等；
（1）请采用计算器模拟实验的方法，帮质量检查员抽取被检产品；
（2）如果没有计算器，你能用什么方法抽取被检产品？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com