
【题目】(1)如图1,等腰Rt△ABO放在平面直角坐标系中, 点A,B 的坐标分别是A(0,1),B(1,0).在x轴正半轴上取D(m,0),在AD右上方作等腰Rt△ADE,∠ADE=![]() .
.
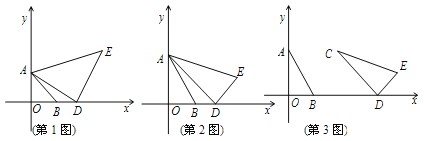
①求出E点的坐标(可用含m的代数式表示);
②证明对于任意正数m,点E都在直线![]() 上;
上;
(2)将(1)中的两个等腰直角三角形都改为有一个角为![]() 的直角三角形,如图22-2,A(0,
的直角三角形,如图22-2,A(0,![]() ),B(1,0). Rt△ADE中, ∠ADE=
),B(1,0). Rt△ADE中, ∠ADE=![]() ,∠AED=
,∠AED=![]() . D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
. D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
(3)将(2)中Rt△AOB保持不动,取点C(2, ![]() ),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=
),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=![]() ,∠CED=
,∠CED=![]() .当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
.当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
【答案】(1)、①、E(m+1,m);②、证明过程见解析;(2)、y=![]() x-
x-![]() ;(3)、y=
;(3)、y=![]() x-
x-![]() .
.
【解析】
试题分析:(1)、过点E作EH⊥x轴,根据等腰直角三角形得到AD=DE,∠OAD=∠EDH, ∠ADO=∠DEH,从而得出△AOD≌△DHE,求出点E的坐标,然后将点代入直线解析式,说明其正确性;(2)、过E作EH⊥x轴于H ,得出△AOD和△DHE相似,根据30°角的直角三角形关系得出点E的坐标,然后求出直线解析式;(3)、将Rt△AOB右移两个单位,得Rt△CFG, 根据(2)的解答,把(2)中的直线右移两个单位即可.
试题解析:(1)、①过E作EH⊥x轴于H,在等腰Rt△ADE中,∠ADE=90°,AD=DE,
∵∠AOB=90° ∴∠OAD=∠EDH, ∠ADO=∠DEH ∴ △AOD≌△DHE ∴DH=AO=1,EH=DO=m, ∴E(m+1,m)
②当x=m+1时, y=x-1=m+1-1=m ∴不论m取何值,E都在直线y=x-1上.
(2)、过E作EH⊥x轴于H 在Rt△ADE中,∠ADE=90°,∵∠AOB=90° ∴∠OAD=∠EDH, ∠ADO=∠DEH
∴△AOD∽△DHE ∴DH:AO=EH:OD=DE:AD=1:![]() ∴DH=1, EH=
∴DH=1, EH=![]() m ∴E(m+1,
m ∴E(m+1, ![]() m)
m)
y=![]() x-
x-![]()
(3)、将Rt△AOB右移两个单位,得Rt△CFG 根据(2)的解答,把(2)中的直线右移两个单位即可
得到: y=![]() x-
x-![]()


科目:初中数学 来源: 题型:
【题目】把弯曲的道路改直,就能缩短路程,其中蕴含的数学原理是( )
A. 过一点有无数条直线 B. 两点确定一条直线
C. 两点之间线段最短 D. 线段是直线的一部分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程kx2-2x+1=0有实数根,则k的取值范围是( )
A. k<1 B. k≤1 C. k<1且k≠0 D. k≤1且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680 000 000元,这个数用科学记数法表示正确的是( )
A. 6.8×109元 B. 6.8×108元 C. 6.8×107元 D. 6.8×106元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查采用了抽样调查的方式
②7万名考生是总体
③1000名考生是总体的一个样本
④每名考生的数学成绩是个体.
A. 2 B. 3 C. 4 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过![]() .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于![]() .
.

(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(-7,9),B(0,9)的抛物线![]() (a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
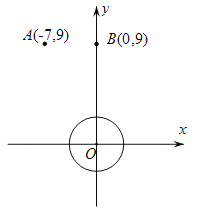
(1)若点D的坐标为D(3,0).①请直接写出此时直线AD与⊙O的位置关系;②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若![]() .
.
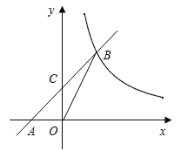
(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
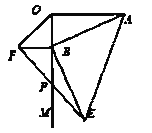
【题目】如图,AO![]() OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com