练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(－2，0)，与反比例函数在第一象限内的图象交于点B（2，n），连结BO，若.

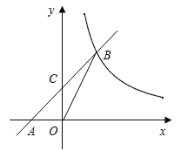
    （1）求该反比例函数的解析式；

    （2）若直线AB与y轴的交点为C，求△OCB的面积.

    【答案】(1)、y=；(2)、

    【解析】

    试题分析：(1)、首先根据OA和△AOB的值得出点B的坐标，然后进行求解；(2)、首先求出直线AB的函数解析式，然后得出点C的坐标，最后计算△OCB的面积.

    试题解析：(1)、根据题意可得OA=2，△AOB的面积为4，则点B的坐标为(2,4)

    将(2,4)代入反比例函数解析式可得：k=8 ∴反比例函数的解析式为y=.

    设直线AB的解析式为y=kx+b，将A(－2,0)和B(2,4)代入得：

    解得： ∴直线AB的解析式为：y=x+2

    ∴点C的坐标为(0,2) ∴△OCB的面积=2×2÷2=2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是 ( )

    A. 立方根是它本身的数只能是0和1 B. 如果一个数有立方根，那么这个数也一定有平方根

    C. 16的平方根是4 D. -2是4的一个平方根 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A(0，1)，B(1，0).在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=.

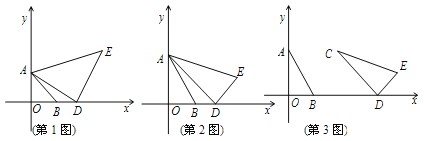
    ①求出E点的坐标(可用含m的代数式表示)；

    ②证明对于任意正数m，点E都在直线上；

    (2)将(1)中的两个等腰直角三角形都改为有一个角为的直角三角形,如图22-2，A(0,)，B(1，0). Rt△ADE中, ∠ADE=,∠AED=. D（m,0）是x轴正半轴上任意一点,则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；

    (3)将(2)中Rt△AOB保持不动,取点C(2, ),在x轴正半轴上取D（m,0）(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=，∠CED=.当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是(　　)

    A.平行四边形的对角线互相平分且相等B.矩形的对角线相等且互相平分

    C.菱形的对角线互相垂直且相等D.正方形的对称轴是正方形的对角线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：xy2﹣x=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝－2x2的开口方向是______，它的形状与y＝2x2的形状______，它的顶点坐标是______，对称轴是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A为数轴上表示-1的点，将点A在数轴上向右平移4个单位长度到点B，则点B表示的有理数为（ ）

    A. 3 B. 2 C. -4 D. 2或-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】等腰三角形的一个角是50°，则它的底角是（ ）
    A.50°
    B.50°或65°
    C.80°
    D.65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图象如图所示，有下列5个结论：① ；② ；③ ；④ ； ⑤ ，（的实数）其中正确的结论有

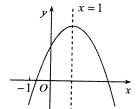
    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    同步练习册答案