
【题目】如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(-7,9),B(0,9)的抛物线![]() (a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
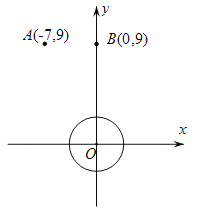
(1)若点D的坐标为D(3,0).①请直接写出此时直线AD与⊙O的位置关系;②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
【答案】(1)、相交;y=-![]() -
-![]() x+9;(2)、
x+9;(2)、![]() ;(3)、
;(3)、![]() .
.
【解析】
试题分析:(1)、根据图形得出圆与直线的位置关系;利用待定系数法求出函数解析式;(2)、分别过点A作圆的两条切线,然后根据△OGD∽△AHD得出AD的长度,然后根据Rt△AHD的勾股定理求出m的值,然后分别将m的值代入函数解析式求出a的值;(3)、根据题意首先求出直线与圆相切时a的值,然后得出相交的取值范围.
试题解析:(1)、①填空:此时直线AD与⊙O的位置关系为 相交
②因为抛物线过A(-7,9),B(0,9) D(3,0).可设设抛物线解析式为![]()
得:![]() 解得: y=-
解得: y=-![]() -
-![]() x+9
x+9
(2)、如图,过A有两条圆的切线,切点为G,连OG,过A作AH⊥x轴.
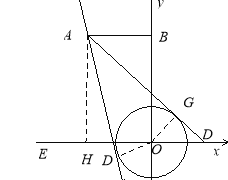
则∵∠OGD=90=∠AHD ∠ADH=∠ADH
∴△OGD∽△AHD ∴OG:OD=AH:AD ∵OG=3,AH=9,OD=|m| ∴AD=3|m|
在Rt△AHD中,![]() 得:
得:![]() ∴
∴![]()
事实上,对于两条射线都有一样的相似和同一个方程,所以上述各个值都符合条件.
设函数关系式为![]() 将点(5,0)和(
将点(5,0)和(![]() 分别代入,得到
分别代入,得到
![]()
(3)、 ![]()


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰Rt△ABO放在平面直角坐标系中, 点A,B 的坐标分别是A(0,1),B(1,0).在x轴正半轴上取D(m,0),在AD右上方作等腰Rt△ADE,∠ADE=![]() .
.
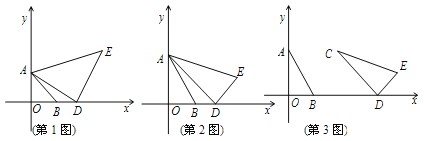
①求出E点的坐标(可用含m的代数式表示);
②证明对于任意正数m,点E都在直线![]() 上;
上;
(2)将(1)中的两个等腰直角三角形都改为有一个角为![]() 的直角三角形,如图22-2,A(0,
的直角三角形,如图22-2,A(0,![]() ),B(1,0). Rt△ADE中, ∠ADE=
),B(1,0). Rt△ADE中, ∠ADE=![]() ,∠AED=
,∠AED=![]() . D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
. D(m,0)是x轴正半轴上任意一点,则不论m取何正数,点E都在某一条直线上,请求出这条直线的函数关系式;
(3)将(2)中Rt△AOB保持不动,取点C(2, ![]() ),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=
),在x轴正半轴上取D(m,0)(m>2), 然后在AD右上方作Rt△CDE, ∠CDE=![]() ,∠CED=
,∠CED=![]() .当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
.当m取不同值时,点E是否还是总在一条直线上? 若是,请求出直线对应的函数关系式,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.平行四边形的对角线互相平分且相等B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等D.正方形的对称轴是正方形的对角线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com