
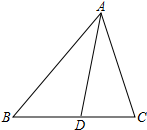
 如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.
如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$. 分析 过点C作CM⊥AD于点M,延长CM交AB于点E,过点E作EF∥AD交BC于点F,则△ACE为等边三角形,根据等边三角形的性质即可得出AM、BE的长度,设DM=x,则EF=2x,再根据平行线的性质即可得出$\frac{BE}{AB}=\frac{EF}{AD}$,代入数据解分式方程即可得出x值,将其代入AD=AM+DM中即可求出AD的长度.
解答 解:过点C作CM⊥AD于点M,延长CM交AB于点E,过点E作EF∥AD交BC于点F,如图所示.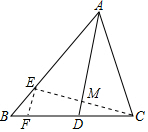
∵∠BAC=60°,∠BAC的平分线交BC于D,AB=8,AC=6,
∴△ACE为等边三角形,BE=AB-AC=2,
∴AM=$\frac{\sqrt{3}}{2}$AC=3$\sqrt{3}$.
设DM=x,则EF=2x,
∵EF∥AD,
∴$\frac{BE}{AB}=\frac{EF}{AD}$,即$\frac{2}{8}=\frac{2x}{3\sqrt{3}+x}$,
解得:x=$\frac{3\sqrt{3}}{7}$,
经检验,x=$\frac{3\sqrt{3}}{7}$是原方程的解,
∴AD=AM+DM=$\frac{24\sqrt{3}}{7}$.
故答案为:$\frac{24\sqrt{3}}{7}$.
点评 本题考查了等边三角形的性质、平行线的性质以及解分式方程,通过解分式方程求出DM的长度是解题的关键.


科目:初中数学 来源: 题型:填空题
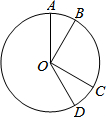 如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则$\widehat{AD}$的长为$\frac{5}{2}$π.(结果保留π)
如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则$\widehat{AD}$的长为$\frac{5}{2}$π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
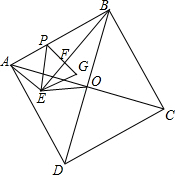 如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠AEB=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{30-3\sqrt{10}}{20}$.
如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠AEB=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{30-3\sqrt{10}}{20}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
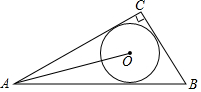 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
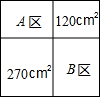 小区内有一块正方形空地,物业计划利用这块空地修建居民休闲区,具体规划如图所示,其中A,B为活动区域,剩余两个正方形区域为绿化区域,面积分别是270m2和120m2,则A,B两个活动区域的总面积为360m2.
小区内有一块正方形空地,物业计划利用这块空地修建居民休闲区,具体规划如图所示,其中A,B为活动区域,剩余两个正方形区域为绿化区域,面积分别是270m2和120m2,则A,B两个活动区域的总面积为360m2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com