
分析 根据二次根式有意义的条件可得关于x的不等式组,解不等式组求得x的值,将x的值代回等式求得y的值,继而可得xy+yx的值.
解答 解:根据题意知,$\left\{\begin{array}{l}{{x}^{2}-4≥0}\\{{4}^{2}-x≥0}\\{2+x≠0}\end{array}\right.$,
解得:x=2,
将x=2代入y=$\sqrt{{x}^{2}-4}$+$\sqrt{4-{x}^{2}}$+$\frac{{x}^{2}+x+8}{2+x}$,得:y=$\frac{7}{2}$,
则x$\sqrt{y}$+y$\sqrt{x}$-$\sqrt{56}$=2$\sqrt{\frac{7}{2}}$+$\frac{7}{2}$$\sqrt{2}$-$\sqrt{56}$=$\frac{7\sqrt{2}}{2}$-$\sqrt{14}$.
点评 本题主要考查二次根式有意义的条件,熟知二次根式有意义的条件是被开方数为非负数是解题的关键.


科目:初中数学 来源: 题型:填空题
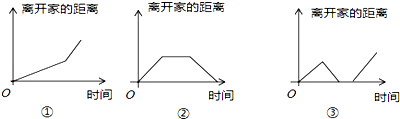
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
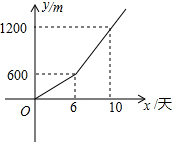 (1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.
(1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
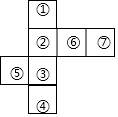 小刚在纸上画了一个长方体的展开图,展开图由长方形和正方形构成,淘气的小明在图上又添加了一个四边形,并把这7个面任意标上了①~⑦的序号(如图).
小刚在纸上画了一个长方体的展开图,展开图由长方形和正方形构成,淘气的小明在图上又添加了一个四边形,并把这7个面任意标上了①~⑦的序号(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com