
【题目】如图,平面直角坐标系xOy中,已知点A(0,3),点B(![]() ,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点C1(-2,![]() ),点C2(0,-2),点C3(
),点C2(0,-2),点C3(![]() ,
,![]() )中,线段AB的“等长点”是点 ;
)中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值;
(3)若直线![]() 上至少存在一个线段AB的“等长点”,直接写出k的取值范围.
上至少存在一个线段AB的“等长点”,直接写出k的取值范围.

【答案】(1)C1,C3 ;(2)m=![]() ,n=0或m=
,n=0或m=![]() ,n=3.(3)
,n=3.(3)![]()
【解析】分析:(1)直接利用线段AB的“等长点”的条件判断;
(2)分两种情况讨论,利用对称性和垂直的性质即可求出m,n;
(3)先判断出直线y=kx+3![]() 与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
本题解析:
(1)C1,C3
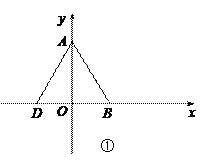
(2)如图①,∵点D(m,n)是线段AB的“等长点”,且∠DAB=60°,
∴△ABD是等边三角形.∵OA=3,
OB=![]() ,∠AOB=90°,∴tan∠ABO=
,∠AOB=90°,∴tan∠ABO=![]() ,
,
∴∠ABO=60°,∠BAO=30°,
∴点D在x轴上,且DB=AB=2![]() ,
,
∴m=-![]() ,n=0.
,n=0.
如图②,同理可知△ABD是等边三角形,∵∠DAB=60°,∠BAO=30°,∴∠DAO=90°,又∵DA=AB=2![]() ,
,
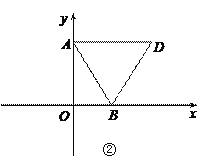 ∴m=2
∴m=2![]() ,n=3.
,n=3.
综上所述,m=-![]() ,n=0或m=2
,n=0或m=2![]() ,n=3.
,n=3.
(3)如图2,∵直线y=kx+3![]() k=k(x+3
k=k(x+3![]() ),
),
∴直线y=kx+3![]() k恒过一点P(3
k恒过一点P(3![]() ,0),
,0),
∴在Rt△AOP中,OA=3,OP=3![]() ,
,
∴∠APO=30°,
∴∠OPA=60°,
∴∠BAP=90°,
当PF与⊙B相切时交y轴于F,
∴PA切⊙B于A,
∴点F就是直线y=kx+33√k与⊙B的切点,
∴F(0,3),
∴33√k=3,
∴k=3√3,
当直线y=kx+3![]() k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
∴△AEG∽△POG,
∴![]() ,
,
∴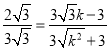 ,
,
∴k=![]() (舍)或k=
(舍)或k=![]() ,
,
∵直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,
k上至少存在一个线段AB的“等长点”,
∴![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.

为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数

表2:小王抽样调查单位10名职工的健康指数

表3:小李抽样调查单位10名职工的健康指数

根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为
(2)小张、小王和小李三人中, 的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在AB边上,AD=CD,DE⊥AC于点E,CF∥AB,交DE的延长线于点F.
(1)如图1,求证:四边形ADCF是菱形; 
(2)如图2,当∠ACB=90°,∠B=30°时,在不添加辅助线的情况下,请直接写出图中与线段AC相等的线段(线段AC除外). 
查看答案和解析>>
科目:初中数学 来源: 题型:
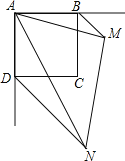
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知多项式x4﹣y+3xy﹣2xy2﹣5x3y3﹣1,按要求解答下列问题:
(1)指出该多项式的项;
(2)该多项式的次数是 ,三次项的系数是 .
(3)按y的降幂排列为: .
(4)若|x+1|+|y﹣2|=0,试求该多项式的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com