
分析 (1)将分式方程转化成整式方程,解整式方程可得出x=1,再将x=1代入原分式方程验证x=1是否为分式方程的解;
(2)解不等式组中的第一个不等式可得出x>$\frac{1}{3}$;解不等式组中的第二个不等式可得出x<$\frac{2}{3}$,将两者合并到一起即可得出结论.
解答 解:(1)去分母,得:x-3+x-2=-3,
整理,得:2x=2,
∴x=1.
经检验,x=1是原方程得解,
∴分式方程$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$的解为x=1.
(2)解不等式2x>1-x,得:x>$\frac{1}{3}$;
解不等式4x+2<x+4,得:x<$\frac{2}{3}$.
∴不等式组的解集为$\frac{1}{3}$<x<$\frac{2}{3}$.
点评 本题考查了解分式方程以及解一元一次不等式组,解题的关键是:(1)得出方程的解后代入原分式方程去验证是否为增根;(2)通过分别接不等式组中的不等式得出不等式的解集.本题属于基础题,难度不大,解决该题型题目时,牢记解分式方程和不等式组的方法是关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
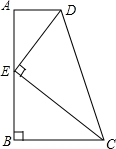 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )| A. | CE=$\sqrt{3}$DE | B. | CE=$\sqrt{2}$DE | C. | CE=3DE | D. | CE=2DE |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com