练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y1= （x＞0）的图象上，顶点B在函数y2= （x＞0）的图象上，∠ABO=30°，则 = ．

    【答案】﹣
    【解析】解：如图，
    Rt△AOB中，∠B=30°，∠AOB=90°，
    ∴∠OAC=60°，
    ∵AB⊥OC，
    ∴∠ACO=90°，
    ∴∠AOC=30°，
    设AC=a，则OA=2a，OC= a，
    ∴A（ a，a），
    ∵A在函数y1= （x＞0）的图象上，
    ∴k1= aa= ，
    Rt△BOC中，OB=2OC=2 a，
    ∴BC= =3a，
    ∴B（ a，﹣3a），
    ∵B在函数y2= （x＞0）的图象上，
    ∴k2=﹣3a a=﹣3 ，
    ∴ =﹣ ；
    所以答案是：﹣ ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，C、D是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于（ ）
    A.40°
    B.50°
    C.60°
    D.70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017通辽）小兰和小颖用下面两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形，转动两个转盘各一次，若两次指针所指数字之和小于4，则小兰胜，否则小颖胜（指针指在分界线时重转），这个游戏对双方公平吗？请用树状图或列表法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把等边△A BC沿着D E折叠，使点A恰好落在BC边上的点P处，且DP⊥BC，若BP=4cm，则EC=cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2 ．
    （1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ， OC△OA=；

    （2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；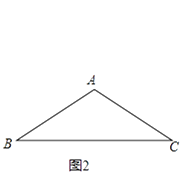

    （3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，Rt△PAB的直角顶点P（3，4）在函数y= （x＞0）的图象上，顶点A、B在函数y= （x＞0，0＜t＜k）的图象上，PA∥x轴，连接OP，OA，记△OPA的面积为S△OPA ， △PAB的面积为S△PAB ， 设w=S△OPA﹣S△PAB ． ①求k的值以及w关于t的表达式；
    ②若用wmax和wmin分别表示函数w的最大值和最小值，令T=wmax+a2﹣a，其中a为实数，求Tmin ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在水域上建一个演艺广场，演艺广场由看台Ⅰ，看台Ⅱ，三角形水域ABC，及矩形表演台BCDE四个部分构成（如图），看台Ⅰ，看台Ⅱ是分别以AB，AC为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍，矩形表演台BCDE 中，CD=10米，三角形水域ABC的面积为 平方米，设∠BAC=θ．
    （1）求BC的长（用含θ的式子表示）；
    （2）若表演台每平方米的造价为0.3万元，求表演台的最低造价．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=4 ，则S阴影= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，AB和DE是直立在地面上的两根立柱，AB=5m，某一时刻AB在阳光下的投影BC=3m．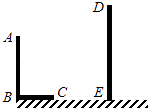
    （1）请你在图中画出此时DE在阳光下的投影；
    （2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长．

    查看答案和解析>>

    同步练习册答案