
【题目】如图所示,Rt△PAB的直角顶点P(3,4)在函数y= ![]() (x>0)的图象上,顶点A、B在函数y=
(x>0)的图象上,顶点A、B在函数y= ![]() (x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
(x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin . 
【答案】解:①∵点P(3,4), ∴在y= ![]() 中,当x=3时,y=
中,当x=3时,y= ![]() ,即点A(3,
,即点A(3, ![]() ),
),
当y=4时,x= ![]() ,即点B(
,即点B( ![]() ,4),
,4),
则S△PAB= ![]() PAPB=
PAPB= ![]() (4﹣
(4﹣ ![]() )(3﹣
)(3﹣ ![]() ),
),
如图,延长PA交x轴于点C,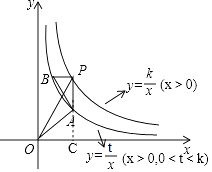
则PC⊥x轴,
又S△OPA=S△OPC﹣S△OAC= ![]() ×3×4﹣
×3×4﹣ ![]() t=6﹣
t=6﹣ ![]() t,
t,
∴w=6﹣ ![]() t﹣
t﹣ ![]() (4﹣
(4﹣ ![]() )(3﹣
)(3﹣ ![]() )=﹣
)=﹣ ![]() t2+
t2+ ![]() t;
t;
②∵w=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣6)2+
(t﹣6)2+ ![]() ,
,
∴wmax= ![]() ,
,
则T=wmax+a2﹣a=a2﹣a+ ![]()
![]() )2+
)2+ ![]() ,
,
∴当a= ![]() 时,Tmin=
时,Tmin= ![]() .
.
【解析】(1)由点P的坐标表示出点A、点B的坐标,从而得S△PAB= ![]() PAPB=
PAPB= ![]() (4﹣
(4﹣ ![]() )(3﹣
)(3﹣ ![]() ),再根据反比例系数k的几何意义知S△OPA=S△OPC﹣S△OAC=6﹣
),再根据反比例系数k的几何意义知S△OPA=S△OPC﹣S△OAC=6﹣ ![]() t,由w=S△OPA﹣S△PAB可得答案;(2)将(1)中所得解析式配方求得wmax=
t,由w=S△OPA﹣S△PAB可得答案;(2)将(1)中所得解析式配方求得wmax= ![]() ,代入T=wmax+a2﹣a配方即可得出答案.
,代入T=wmax+a2﹣a配方即可得出答案.
【考点精析】掌握比例系数k的几何意义是解答本题的根本,需要知道几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


科目:初中数学 来源: 题型:
【题目】如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.
(1)①请画出△ABC关于y轴对称的△A1B1C1;
②画出△A1B1C1向下平移3个单位得到的△A2B2C2;
(2)若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.
(1)判断四边形ACC'A'的形状,并说明理由;
(2)在△ABC中,∠B=90°,A B=24,cos∠BAC= ![]() ,求CB'的长.
,求CB'的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1= ![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF. 
(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() 的图象如图所示,以下结论: ①常数m<﹣1;
的图象如图所示,以下结论: ①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC. 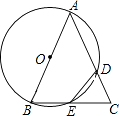
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( ) 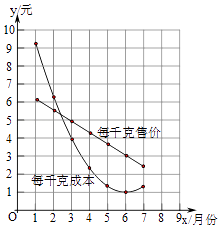
A.1月份
B.2月份
C.5月份
D.7月份
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com