练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，已知平行四边形ABCD中，点E是对角线AC上的一点，且满足AE：EC=1：3，连接BE并延长，交AD于点G，交CD的延长线于点F，求AG：GD的值．

    分析 由平行四边形ABCD的性质推知AD∥BC，且AD=BC，则易得△AEG∽△CEB，由相似三角形的对应边成比例得到AG：BC的值，继而求得AG：GD的值．

    解答 解：∵四边形ABCD是平行四边形，
    ∴AD∥BC，且AD=BC，
    ∴△AEG∽△CEB，
    ∴$\frac{AE}{EC}$=$\frac{AG}{BC}$，即$\frac{1}{3}$=$\frac{AG}{BC}$，
    ∴$\frac{1}{3}$=$\frac{AG}{AD}$，
    ∴AG：GD=1：2．

    点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．如图，△ABC内接于⊙O，AB=AC，过点C作⊙O的直径CD，连接BD．
    （1）求证：∠BDC=2∠ABD；
    （2）连接OA，求证：OA∥BD；
    （3）在（2）的条件下，过点D作DE⊥AB，垂足为E，延长DE交AC于F，当F为AC的中点时，若DE=4，求OF的长．

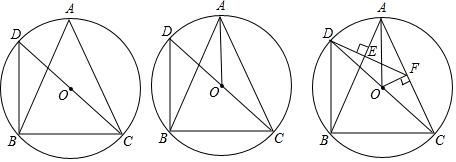
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

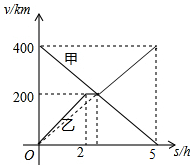    17．甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲，乙两车距B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲，y乙与x之间的函数图象如图所示，结合图象解答下列问题：
    （1）甲车的速度是80km/h，乙车休息了0.5h；
    （2）求乙车与甲车相遇后y乙关于x的函数解析式，并写出自变量x的取值范围；
    （3）当甲车出发多少小时后，两车相距80km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

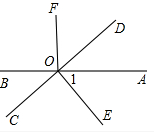    14．如图，直线AB、CD相交于O，OD平分∠AOF，OE⊥CD于点O，∠1=50°，求∠BOC、∠BOF的度数．
    解：∵OE⊥CD（已知）
    ∴∠DOE=90°（垂直的定义）
    ∵∠1=50°（已知）
    ∴∠AOD=∠DOE-∠1=40°
    ∵∠BOC与∠AOD为对顶角（已知）
    ∴∠BOC=∠AOD=∠40°（对顶角相等）
    ∵OD平分∠AOF（已知）
    且∠AOD=40°（已求）
    ∴∠AOF=2∠AOD=80°（角平分线定义）
    ∵∠BOF+∠AOF=180°（邻补角定义）
    ∴∠BOF=180°-∠AOF=100°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

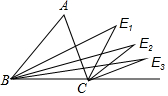    1．如图，∠A=60°，BE1平分∠ABC，CE1平分∠ACD，则∠E1=30°；BE2平分∠E1BC，CE2平分∠E1CD，则∠E2=15°；…；BEn平分∠En-1BC，CEn平分∠En-1CD，则∠En=$\frac{60°}{{2}^{n}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，将图1的正方形纸片沿对角线剪开，得到图2的两张三角形纸片，再将三角形纸片摆成图3所示的图形，使得点B（E）重合．
    （1）求证：△ABD≌△CBF；
    （2）猜测AD与CF的位置关系，并说明理由；
    （3）若∠ABF=120°，请判断△BGH的形状，并说明理由．

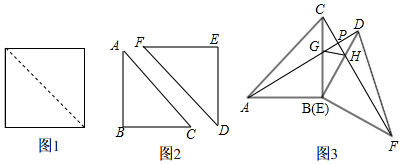
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

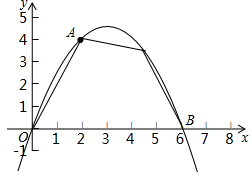    2．如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某商场计划投入一笔资金采购一批紧俏商品，经过市场调查发现，如果月初出售，可获利15%，并可用本金和利润再投资其他商品，到月末又可获利10%；如果月末出售可获利30%，但要付出仓储费用700元．
    （1）若商场投资x元，分别用含x的代数式表示月初出售和月末出售所获得的利润；
    （2）若商场投资40000元，问选择哪种销售方式获利较多？此时获利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．2016年9月底，雪山镇风力电站每天能发电约74850000度，该数据用科学记数法表示为7.485×107 度．

    查看答案和解析>>

    同步练习册答案