
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为 . 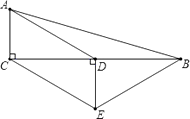
【答案】10+2 ![]()
【解析】解:∵∠ACB=90°,DE⊥BC, ∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,
∴BC=2CD=4 ![]() ,
,
在△ABC中,∠ACB=90°,
由勾股定理得AB= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2 ![]() ,
,
所以答案是:10+2 ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和三角形中位线定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD=BC,AB=CD
C.AB∥CD,AD=BC
D.∠A=∠C,∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证: ![]() ;
;
(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=9,DA=DC=12,∠BAD=90°,DE⊥CF.求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
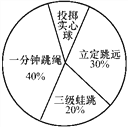
【题目】
某校九年级一班共40名学生,需要参加体育“四选一”自选项目测试,如图是该班学生所报自选项目人数的扇形统计图,请根据图中信息,完成下面各题:
(1) 图中“投掷实心球”所在扇形对应的圆心角的度数为 度;该班自选项目为“投掷实心球”的学生共有 名;
(2)在自选项目为“投掷实心球”的学生中,只有1名女生.为了了解学生的训练效果,将从自选项目为“投掷实心球”的学生中,随机抽取2名学生进行投掷实心球训练测试,请用树状图或列表法求所抽取的2名学生中恰好有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,点E、F同时从点C出发,以![]() cm/s的速度分别沿CA、CB匀速运动,当点E到达点 A时,两点同时停止运动,设运动时间为ts.过点F作BC的垂线l交AB于点D,点G与点E关于直线l对称.
cm/s的速度分别沿CA、CB匀速运动,当点E到达点 A时,两点同时停止运动,设运动时间为ts.过点F作BC的垂线l交AB于点D,点G与点E关于直线l对称.
(1)当t = s时,点G在∠ABC的平分线上;
(2)当t = s时,点G在AB边上;
(3)设△DFG与△DFB重合部分的面积为Scm2, 求S与t之间的函数关系式,并写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com