练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列条件不能判定四边形ABCD是平行四边形的是（ ）
    A.AB∥CD，AD∥BC
    B.AD=BC，AB=CD
    C.AB∥CD，AD=BC
    D.∠A=∠C，∠B=∠D

    【答案】C
    【解析】解：A、根据平行四边形的判定定理：两组对边分别平行的四边形是平行四边形，故能判断这个四边形是平行四边形，不合题意； B、根据平行四边形的判定定理：两组对边分别相等的四边形是平行四边形，故能判断这个四边形是平行四边形，不合题意；
    C、不能判断这个四边形是平行四边形，符合题意；
    D、根据平行四边形的判定定理：两对角相等的四边形是平行四边形，故能判断这个四边形是平行四边形；
    故选：C．

    【考点精析】本题主要考查了平行四边形的判定的相关知识点，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

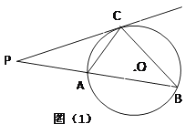
    【题目】已知，如图(1)， 为⊙的割线，直线与⊙有公共点, 且,

    （1）求证： ; 直线是⊙的切线；

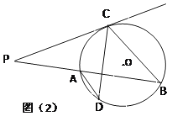
    （2）如图（2） , 作弦，使 连接AD、BC,若，求⊙的半径；

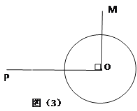
    （3）如图（3），若⊙的半径为，,,,⊙上是否存在一点 , 使得有最小值？若存在，请求出这个最小值；若不存在，说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某空调生产厂家想了解一批空调的质量，把仓库中的空调编上号，然后抽取了编号为5的倍数的空调进行检验，你认为这种调查方式________．(填“合适”或“不合适”)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．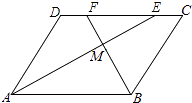
    （1）试说明：AE⊥BF；
    （2）判断线段DF与CE的大小关系，并予以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．
    （下面是彬彬同学进行的推理，请你将彬彬同学的推理过程补充完整．）
    解：∵AB∥CD （已知）
    ∴∠A=（两直线平行，内错角相等）
    又∵∠A=∠D（）
    ∴ =（等量代换）
    ∴AC∥DE （）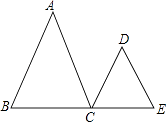

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且F恰好为DC的中点，DG⊥AE，垂足为G．若DG=1，则AE的长为（ ）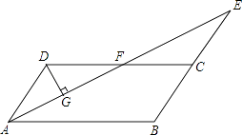
    A.2
    B.4
    C.4
    D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．

    （1）求证：直线PA为⊙O的切线；

    （2）试探究线段EF，OD，OP之间的等量关系，并加以证明；

    （3）若BC＝6，tan∠F＝，求cos∠ACB的值和线段PE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4，则四边形ACEB的周长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况，给他出了一道题：如图，AB∥DE，∠B=80°，CM平分∠BCD，CN⊥CM，求∠NCE的度数．“大头儿子”稍加思索，就做出来了，你知道他是怎样解的吗？请把你的推理过程写下来吧．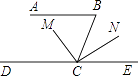

    查看答案和解析>>

    同步练习册答案