
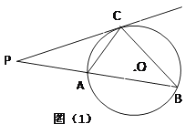
【题目】已知,如图(1), ![]() 为⊙
为⊙![]() 的割线,直线
的割线,直线![]() 与⊙
与⊙![]() 有公共点
有公共点![]() , 且
, 且![]() ,
,
(1)求证: ![]() ; 直线
; 直线![]() 是⊙
是⊙![]() 的切线;
的切线;
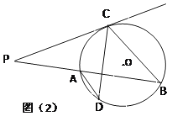
(2)如图(2) , 作弦![]() ,使
,使![]() 连接AD、BC,若
连接AD、BC,若![]() ,求⊙
,求⊙![]() 的半径;
的半径;
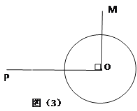
(3)如图(3),若⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,⊙
,⊙![]() 上是否存在一点
上是否存在一点![]() , 使得
, 使得![]() 有最小值?若存在,请求出这个最小值;若不存在,说明理由。
有最小值?若存在,请求出这个最小值;若不存在,说明理由。
【答案】(1) 证明见解析; 证明见解析; (2) R=![]() ;(3)
;(3)![]() 最小值为
最小值为![]()
【解析】试题分析:(1)根据已知条件得到![]() ,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;
,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;
(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,推出AE∥CD,得到![]() ,根据勾股定理得到BE=2
,根据勾股定理得到BE=2![]() ,于是得到结论;
,于是得到结论;
(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,得到OG=![]() OM=1,根据相似三角形的性质得到
OM=1,根据相似三角形的性质得到![]() ,求得QG=
,求得QG=![]() QM,根据两点之间线段最短,即可得到结论.
QM,根据两点之间线段最短,即可得到结论.
试题解析:(1)①证明:∵PC2=PA×PB,
∴![]() ,
,
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
②作直径CF,连接AF,则∠CAF=90°,

∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,
∴直线PC是⊙O的切线;
(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
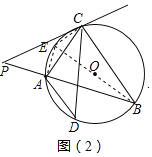
∵CD⊥AB,
∴AE∥CD,
∴![]() ,
,
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2![]() ,
,
∴R=![]() ;
;
(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,
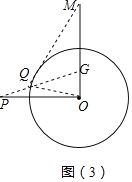
∵MO=2,
∴OG=![]() OM=1,
OM=1,
∵⊙O的半径r=OQ=![]() ,
,
∴OQ2=OGOM,
∵∠MOQ=∠QOG,
∴△MOQ∽△QOG,
∴![]() ,
,
∴QG=![]() QM,
QM,
∴PQ+![]() QM=PQ+QG=PG,
QM=PQ+QG=PG,
根据两点之间线段最短,
此时PQ+![]() QM=PQ+QG=PG最小,
QM=PQ+QG=PG最小,
∴PQ+![]() QM最小值为PG=
QM最小值为PG=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴. 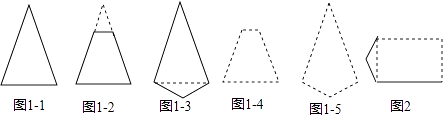
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.数据收集整理后,绘制了图1和图2两幅不完整的统计图,请根据统计图中的信息解答下列问题:
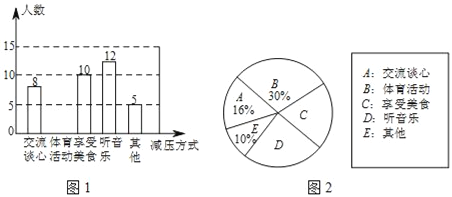
(1)请通过计算,补全条形统计图;
(2)请直接写出扇形统计图中“享受美食”所对应圆心角的度数为 ;
(3)根据调查结果,可估计出该校九年级学生中减压方式的众数和中位数分别是 , .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B左侧),其顶点为P,直线y=kx+b过抛物线与x轴的一个交点A,且与抛物线相交的另外一个交点为C,若S△ABC=10,请你回答下列问题:
(1)求直线的解析式;
(2)求四边形APBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(ax2﹣2xy+y2)﹣(﹣ax2+bxy+2y2)=6x2﹣9xy+cy2成立,则a,b,c的值分别为( )
A. 3,﹣7,﹣1 B. ﹣3,7,﹣1 C. 3,7,﹣1 D. ﹣3,﹣7,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.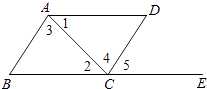
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD=BC,AB=CD
C.AB∥CD,AD=BC
D.∠A=∠C,∠B=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com