
【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 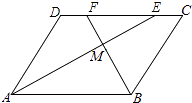
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
【答案】
(1)解:方法一:如图①,
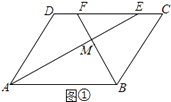
∵在ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
方法二:如图②,延长BC、AE相交于点P,
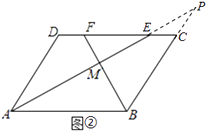
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴AB=BP.
∵BF平分∠ABP,
∴AP⊥BF,
即AE⊥BF
(2)解:方法一:线段DF与CE是相等关系,即DF=CE,
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
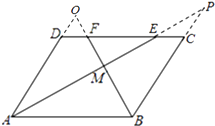
方法二:如图,延长BC、AE设交于点P,延长AD、BF相交于点O,
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴BP=AB.
同理可得,AO=AB.
∴AO=BP.
∵在ABCD中,AD=BC,
∴OD=PC.
又∵在ABCD中,DC∥AB,
∴△ODF∽△OAB,△PCE∽△PBA.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∴DF=CE.
【解析】(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB= ![]() ∠DAB,∠MBA=
∠DAB,∠MBA= ![]() ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B左侧),其顶点为P,直线y=kx+b过抛物线与x轴的一个交点A,且与抛物线相交的另外一个交点为C,若S△ABC=10,请你回答下列问题:
(1)求直线的解析式;
(2)求四边形APBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a、b为有理数,如果规定一种新的运算“⊕”,定义:a⊕b=a2﹣ab+a﹣1,请根据“⊕”的意义计算下列各题:
(1)3⊕6;
(2)(1⊕3)⊕(﹣3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级350名学生的视力情况,从中抽查了80名学生的视力.在这个问题中,总体、个体、样本各是什么?上述问题采用的调查方式是普查还是抽样调查?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD=BC,AB=CD
C.AB∥CD,AD=BC
D.∠A=∠C,∠B=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com