
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴ =(等量代换)
∴AC∥DE ()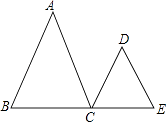
科目:初中数学 来源: 题型:
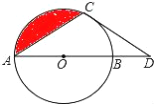
【题目】(12分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3, ![]() 的长为π.
的长为π.
(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已知)
∴∠BFD=∠B(等量代换)
∴AB∥CD()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD=BC,AB=CD
C.AB∥CD,AD=BC
D.∠A=∠C,∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证: ![]() ;
;
(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=9,DA=DC=12,∠BAD=90°,DE⊥CF.求出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com