
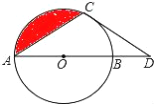
【题目】(12分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3, ![]() 的长为π.
的长为π.
(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.
【答案】(1)相切(2)![]()
【解析】试题分析:(1)、首先连接OC,根据弧的长度得出∠BOC=60°,然后根据等腰三角形的性质得出∠D=∠CAD=30°,从而得出∠OCD=90°,即得出切线;(2)、根据题意得出∠AOC=120°,然后根据阴影部分的面积=扇形AOC的面积减去△AOC的面积得出答案.
试题解析:(1)相切。
理由:连接OC,设∠BOC的度数为n°,则![]() =π,
=π,
解得n=60°,
∴∠A=![]() ∠BOC=30°,
∠BOC=30°,
∵AC=CD,
∴∠A=∠D=30°,
∴∠OCD=180°﹣∠BOC﹣∠D=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
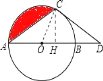
(2)解:作CH⊥OB于H,则CH=OCsin60°=3×![]() =
=![]() ,
,
∵∠BOC=60°,
∴∠AOC=120°,
∴S阴影=S扇形OAC﹣S△OAC=![]() ﹣
﹣![]() ×3×
×3×![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】国家游泳中心﹣﹣“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( )
A.0.26×106
B.26×104
C.2.6×106
D.2.6×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2. 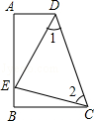
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调生产厂家想了解一批空调的质量,把仓库中的空调编上号,然后抽取了编号为5的倍数的空调进行检验,你认为这种调查方式________.(填“合适”或“不合适”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把﹣1﹣(+4)﹣(﹣3)+(﹣6)+(+2)写成省略加号的和的形式,正确的是( )
A. ﹣1﹣4﹣3﹣6+2 B. ﹣1+4+3﹣6+2 C. ﹣1﹣4+3﹣6+2 D. ﹣1﹣4﹣3+6+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴ =(等量代换)
∴AC∥DE ()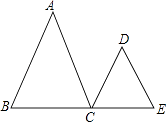
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
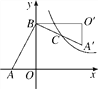
A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com