
【题目】已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为 .
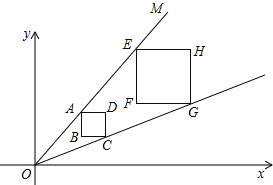
【答案】(9,6).
【解析】
试题分析:先利用待定系数法确定直线OA的解析式为y=mx,根据坐标与图形变换由点A(6,6),正方形ABCD的边长为2得到D点坐标为(8,6),C点坐标为(8,4),再利用待定系数法确定直线OC的解析式为y=![]() x,则可设G点坐标为(t,
x,则可设G点坐标为(t,![]() t),由于正方形EFGH的边长为3,所以H点坐标为(t,
t),由于正方形EFGH的边长为3,所以H点坐标为(t,![]() t+3),从而得到E点坐标为(t﹣3,
t+3),从而得到E点坐标为(t﹣3,![]() t+3),然后把把E点坐标代入y=x求出t=12,得到E点坐标为(9,9),再把E点向下平移3个单位即可得到F点的坐标.
t+3),然后把把E点坐标代入y=x求出t=12,得到E点坐标为(9,9),再把E点向下平移3个单位即可得到F点的坐标.
解:设直线OA的解析式为y=mx,
把A(6,6)代入得6m=6,解得m=1,
∴直线OA的解析式为y=x,
∵点A(6,6),正方形ABCD的边长为2,
∴D点坐标为(8,6),C点坐标为(8,4).
设直线OC的解析式为y=kx,
把C(8,4)代入y=kx
得8k=4,解得k=![]() ,
,
∴直线OC的解析式为y=![]() x,
x,
设G点坐标为(t,![]() t),
t),
∵正方形EFGH的边长为3,
∴H点坐标为(t,![]() t+3),E点坐标为(t﹣3,
t+3),E点坐标为(t﹣3,![]() t+3),
t+3),
把E(t﹣3,![]() t+3)代入y=x
t+3)代入y=x
得t﹣3=![]() t+3,解得t=12,
t+3,解得t=12,
∴E点坐标为(9,9),
∴F点的坐标为(9,6).
故答案为:(9,6).


科目:初中数学 来源: 题型:
【题目】(1)如图所示,小明准备在C处牵牛到河边AB饮水,按下列要求作图并说明理由.
①请用三角板作出小明的最短路线(不考虑其他因素);
②如图乙,若小明在C处牵牛到河边AB饮水,并且必须到河边D处观察河水的水质情况,请作出小明行走的最短路线。

(2)经过平移,图中左边图形上A点移到E点,作出平移后的图形。

理由: ;理由: 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①、②,解答下面各题:
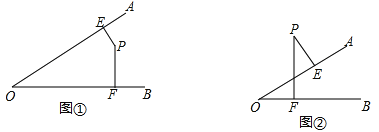
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.

(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,参加调高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com