
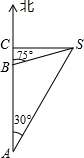
 (2013•莒南县二模)如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东75°,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离.(计算过程和结果一律不取近似值)
(2013•莒南县二模)如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东75°,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离.(计算过程和结果一律不取近似值)
| ||||
| 4 |
| 1 |
| 2 |
| BD |
| sin45° |
| 8 | ||||
|
| 2 |
| 2 |
| ||||
| 4 |
| 2 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 (2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
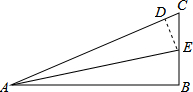 (2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )
(2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com