
分析 (1)根据直角三角形两锐角互余求出∠B,然后求出c=2a,再利用勾股定理列式计算即可得解.
(2)根据直角三角形的性质,可得∠B,根据正弦函数,可得c,再根据勾股定理,可得a的长;
(3)由BC与AB的长,利用勾股定理求出AC的长,利用锐角三角函数定义求出sinA的值,确定出A的度数,由直角三角形两锐角互余,即可求出B的度数.
(4)利用∠B的正弦列式求出b,余弦求出a,再根据直角三角形两锐角互余求出∠A
解答 解:(1)∵∠C=90°,∠A=30°,
∴∠B=60°,
∴c=2a,
∴a=4,
∵c2=a2+b2,
∴b=4$\sqrt{3}$.
(2)由直角三角形的性质,得
∠B=90°-∠A=90°-15°=75°,
sin∠B=sin75°=$\frac{b}{c}=\frac{7}{c}≈0.97$,
c≈7.2,
a=$\sqrt{7.{2}^{2}-{7}^{2}}$≈1.7.
(3)在Rt△ABC中,BC=5,AB=7,
根据勾股定理得:c=$\sqrt{{a}^{2}+{b}^{2}}=13$,
∵sinA=$\frac{a}{c}=\frac{5}{13}$,
∴∠A≈23°,
∴∠B=90°-23°=67°.
(4)b=c•sinB=14×0.9511≈13.315,
a=c•cosB=14×0.3090≈4.326,
∠A=90°-72°=18°.
点评 本题考查了解直角三角形,主要利用了锐角三角函数和勾股定理.


科目:初中数学 来源: 题型:解答题
 如图:在边长为1的正方形网格中有一个△ABC,按要求进行下列解答:
如图:在边长为1的正方形网格中有一个△ABC,按要求进行下列解答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
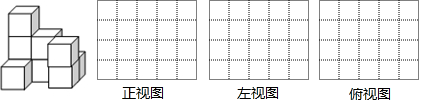
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
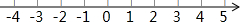 把下列各数在数轴上表示出来,并按从小到大的顺序用“<”连接起来.
把下列各数在数轴上表示出来,并按从小到大的顺序用“<”连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
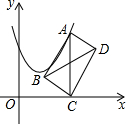 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,点C在x轴上运动,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,点C在x轴上运动,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com