阅读以下材料:
若关于x的三次方程x
3+ax
2+bx+c=0(a、b、c为整数)有整数解n,则将n代入方程x
3+ax
2+bx+c=0得:n
3+an
2+bn+c=0
∴c=-n
3-an
2-bn=-n(n
2+an+b)
∵a、b、n都是整数∴n
2+an+b是整数∴n是c的因数.
上述过程说明:整数系数方程x
3+ax
2+bx+c=0的整数解n只能是常数项c的因数.
如:∵方程x
3+4x
2+3x-2=0中常数项-2的因数为:±1和±2,
∴将±1和±2分别代入方程x
3+4x
2+3x-2=0得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
解决下列问题:
(1)根据上面的学习,方程x
3+2x
2+6x+5=0的整数解可能
±1,±5
±1,±5
;
(2)方程-2x
3+4x
2+12x-14=0有整数解吗?若有,求出整数解;若没有,说明理由.

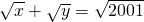 的整数解有
的整数解有 阅读快车系列答案
阅读快车系列答案