Question

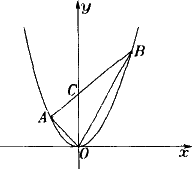
已知抛物线y＝x²和直线y＝(m²－1)x＋m²．(1)当m为何实数时，抛物线与直线有两个交点？(2)设坐标原点为O，抛物线与直线的交点从左到右分别为A、B．如下图所示，当直线与抛物线两交点的横坐标之差为3时，求△AOB中OB边上的高．

Answer 1

答案：
解析：

解：(1)由 　　∴x2－(m2－1)x－m2＝0．　① 　　Δ＝[－(m2－1)]2－4×(－m2)＝(m2＋1)2＞0． 　　∴无论m取任何实数，方式①总有两个不同的实数根， 　　即无论m取任何实数，直线与抛物线总有两个不同的交点． 　　(2)解方程①，有x1＝－1，x2＝m2．令|m2－(－1)|＝3． 　　有m2＋1＝3． 　　∴m＝±， 　　∴当m＝±时，直线与抛物线两交点的横坐标之差为3． 　　此时，y＝x＋2，A(－1，1)，B(2，4)． 　　由勾股定理，得|OA|＝，|OB|＝． 　　过B作x轴的垂线，交x轴于点M，过点A作BM的垂线，交BM于N．则|AN|＝3，|NB|＝3． 　　∴|AB|＝．∵|OA|2＋|AB|2＝|OB|2， 　　∴由勾股定理定理，知△AOB为直角三角形，且∠BAO＝90°． 　　设·＝·h． 　　∴h＝＝＝． 　　思路点拨：(1)联立抛物线和直线方程得方程组，消去一个元y，得到关于x的一元二次方程，方程有两个不同的解，判别式大于零，从而求出m的范围； 　　(2)先由已知条件求出m的值，从而求出点A、B的坐标，从而运用三角形面积公式及等面积法求出解． 　　评注：本题是一道抛物线与三角形结合的几何问题，它主要考查了抛物线的有关概念及三角形中相关知识，比如判断三角形形状、计算三角形面积等．虽然是一道几何题，但最终的解决，还是要转化为代数问题来解，这充分体现了数形结合思想． 　　第(2)题中，计算△OAB的面积还可以这样解： 　　由前解题过程易得，直线AB的方程为y＝x＋2，点A(－1，1)，B(2，4)，|OB|＝， 　　设直线AB与y轴交于点C，则C(0，2)， 　　从而S△OAB＝S△OCA＋S△OCB＝×2×(1＋2)＝3 　　也就是说计算△OAB的面积可用割补思想，这种思想在坐标系中计算几何图形的面积经常使用．需认真领会．