解:(1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H.
∵AB∥CD,
∴DG=CH,DG∥CH.
∴四边形DGHC为矩形,GH=CD=1.
∵DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴△AGD≌△BHC(HL).
∴AG=BH=
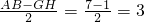
.
∵在Rt△AGD中,AG=3,AD=5,
∴DG=4.
∴S
梯形ABCD=

=16.
(2)∵MN∥AB,ME⊥AB,NF⊥AB,
∴ME=NF,ME∥NF.
∴四边形MEFN为矩形.
∵AB∥CD,AD=BC,
∴∠A=∠B.
∵ME=NF,∠MEA=∠NFB=90°,
∴△MEA≌△NFB(AAS).
∴AE=BF.
设AE=x,则EF=7-2x.
∵∠A=∠A(公共角),∠MEA=∠DGA=90°,
∴△MEA∽△DGA.
∴
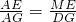
.
∴ME=
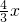
.
∴S
矩形MEFN=ME•EF=

x(7-2x)=-

(x-

)
2+

.
当x=

时,ME=

<4,
∴四边形MEFN面积的最大值为

.
(3)能.
由(2)可知,设AE=x,则EF=7-2x,ME=

x.
若四边形MEFN为正方形,则ME=EF.
即

=7-2x.
解得x=

.
∴EF=7-2x=7-2×

=

<4.
∴四边形MEFN能为正方形,其面积为S
正方形MEFN=(

)
2=
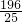
.
分析:(1)本题的关键是求梯形的高,可通过梯形两底的差和腰的长求出梯形的高,然后根据梯形的面积公式即可得出梯形ABCD的面积.
(2)可用二次函数来求解.可设四边形MEFN(其实是矩形)的面积为y,AE=BF=x,那么可根据AB的长表示出EF,然后根据相似三角形△AEM和△AGD得出的关于EM、GD、AE、AG的比例关系式用x表示出ME (也可用∠A的正切函数来求),然后根据矩形的面积公式即可得出y、x的函数关系式,根据函数的性质即可求出y的最大值也就是矩形MEFN的最大面积.
(3)若四边形MEFN为正方形,那么ME=EF,可据此确定x的值,然后将x的值代入(2)的函数式中即可求出正方形MEFN的面积.
点评:本题考查了等腰梯形的性质,矩形的性质,正方形的判定,相似三角形的性质以及二次函数的应用等知识点.综合性较强,考查学生数形结合的数学思想方法.

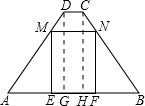
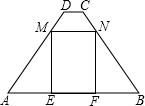 如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M,N分别在边AD,BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E,F.
如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M,N分别在边AD,BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E,F.
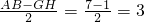 .
. =16.
=16.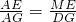 .
.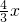 .
. x(7-2x)=-
x(7-2x)=- (x-
(x- )2+
)2+ .
. 时,ME=
时,ME= <4,
<4, .
. x.
x. =7-2x.
=7-2x. .
. =
= <4.
<4. )2=
)2=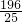 .
.

 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )