
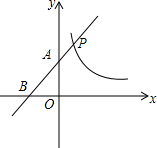
 如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.
如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6. 分析 过点P作PE⊥x轴于E,PF⊥y轴于F,由y=x+m得:A(0,m),B(-m,0),得到OA=m,OB=m,确定△ABO是等腰直角三角形,得到∠ABO=45°,∠BAO=∠ABO=∠FAP=45°,确定△AFP与△PBE也是等腰直角三角形,设P(x,y),则PE=BE=y,PF=AF=x,根据勾股定理得到PA=$\sqrt{2}$x,PB=$\sqrt{2}$y,由点P在y=$\frac{3}{x}$的图形上,求得PA•PB=2xy=2×3=6.
解答 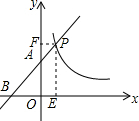 解:过点P作PE⊥x轴于E,PF⊥y轴于F,
解:过点P作PE⊥x轴于E,PF⊥y轴于F,
由y=x+m得:A(0,m),B(-m,0),
∴OA=m,OB=m,
∴△ABO是等腰直角三角形,
∴∠ABO=45°,
∴∠BAO=∠ABO=∠FAP=45°
∴PE=BE,
设P(x,y),则PE=BE=y,PF=AF=x,
∴PA=$\sqrt{2}$x,PB=$\sqrt{2}$y,
∴PA•PB=2xy,
∵点P在y=$\frac{3}{x}$的图形上,
∴PA•PB=2xy=2×3=6,
故答案为:6.
点评 本题主要考查了等腰直角三角形的判定和性质,反比例函数$y=\frac{k}{x}$中k的几何意义,这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{4}{7}$ | C. | $\frac{7}{4}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)3•(-3)4=-37 | B. | (-28)3=(-2)24 | C. | (3×105)2=9×1010 | D. | ${({-3})^5}÷{3^6}=-\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
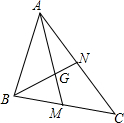 如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com