
分析 通过观察得到:这列数依次可化为$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$…$\frac{1}{n(n+1)}$计算解答即可.
解答 解:(1)$\frac{1}{2}$=$\frac{1}{1×2}$,$\frac{1}{6}$=$\frac{1}{2×3}$,$\frac{1}{12}$=$\frac{1}{3×4}$,$\frac{1}{20}$=$\frac{1}{4×5}$,$\frac{1}{30}$=$\frac{1}{5×6}$,$\frac{1}{42}$=$\frac{1}{6×7}$,$\frac{1}{56}=\frac{1}{7×8}$,$\frac{1}{n(n+1)}$;
(2)$\frac{1}{132}=\frac{1}{11×12}$,所以是第11个数;
(3)$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+$\frac{1}{30}$+$\frac{1}{42}$+…+$\frac{1}{2016×2017}$
=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2016}-\frac{1}{2017}$
=$\frac{2016}{2017}$;
故答案为:$\frac{1}{56}$;$\frac{1}{n(n+1)}$;11.
点评 此题考查了规律型:数字的变化,解此类题目,关键是根据所给的条件找到规律.本题的关键是把数据变形得到分母的规律为n(n+1).


科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
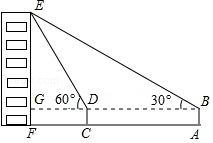 如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)
如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com