
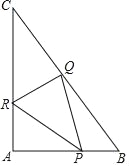
ЁОЬтФПЁПШчЭМЃЌжБНЧЁїABCжаЃЌЁЯAЮЊжБНЧЃЌABЃН6ЃЌACЃН8ЃЎЕуPЁЂQЁЂRЗжБ№дкABЁЂBCЁЂCAБпЩЯЭЌЪБПЊЪМзїдШЫйдЫЖЏЃЌ2УыКѓШ§ИіЕуЭЌЪБЭЃжЙдЫЖЏЃЌЕуPгЩЕуAГіЗЂвдУПУы3ИіЕЅЮЛЕФЫйЖШЯђЕуBдЫЖЏЃЌЕуQгЩЕуBГіЗЂвдУПУы5ИіЕЅЮЛЕФЫйЖШЯђЕуCдЫЖЏЃЌЕуRгЩЕуCГіЗЂвдУПУы4ИіЕЅЮЛЕФЫйЖШЯђЕуAдЫЖЏЃЌгУtЃЈУыЃЉЃЈ0ЁмtЁм2ЃЉБэЪОдЫЖЏЪБМфЃЌдкдЫЖЏЙ§ГЬжаЃК
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAPRЕФУцЛ§ЮЊ4ЃЛ
ЃЈ2ЃЉЧѓГіЁїCRQЕФзюДѓУцЛ§ЃЛ
ЃЈ3ЃЉЪЧЗёДцдкtЃЌЪЙЁЯPQRЃН90ЁуЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() Лђ
Лђ![]() УыЃЛЃЈ2ЃЉЕБtЃН1ЪБЃЌSЁїCQRзюДѓЃН6ЃЛЃЈ3ЃЉtЕФжЕЮЊ1УыЛђ
УыЃЛЃЈ2ЃЉЕБtЃН1ЪБЃЌSЁїCQRзюДѓЃН6ЃЛЃЈ3ЃЉtЕФжЕЮЊ1УыЛђ![]() УыЃЎ
УыЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩдЫЖЏЕУГіAPЃН3tЃЌARЃН8Љ4tЃЌзюКѓгУШ§НЧаЮУцЛ§ЙЋЪННЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШЙЙдьГіжБНЧШ§НЧаЮБэЪОГіQDЃЌзюКѓгУШ§НЧаЮУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіЁїBFPЁзЁїBACЃЌЕУГіFPЃН![]() ЃЈ6Љ3tЃЉЃЌBFЃН
ЃЈ6Љ3tЃЉЃЌBFЃН![]() ЃЈ6Љ3tЃЉЃЌНјЖјFQЃНBQЉBFЃН5tЉ
ЃЈ6Љ3tЃЉЃЌНјЖјFQЃНBQЉBFЃН5tЉ![]() ЃЈ6Љ3tЃЉЃН
ЃЈ6Љ3tЃЉЃН![]()
ЭЌРэЃКEQЃН![]() ЃЌREЃН
ЃЌREЃН![]() ЃЌдйХаЖЯГіЁїREQЁзЁїQFPЃЎЕУГі
ЃЌдйХаЖЯГіЁїREQЁзЁїQFPЃЎЕУГі![]() ЃЌгУREЁСFPЃНQFЁСEQНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЎ
ЃЌгУREЁСFPЃНQFЁСEQНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉгЩдЫЖЏжЊЃЌAPЃН3tЃЌCRЃН4tЃЌ
ЁрARЃН8Љ4tЃЌ
ЁрSЁїAPRЃН![]() APARЃН
APARЃН![]() ЁС3tЁСЃЈ8Љ4tЃЉЃН12tЉ6t2ЃН4ЃЌ
ЁС3tЁСЃЈ8Љ4tЃЉЃН12tЉ6t2ЃН4ЃЌ
НтЕУtЃН![]() ЛђtЃН
ЛђtЃН![]()
ЁрЕБtЮЊ![]() Лђ
Лђ![]() УыЪБЃЌЁїAPRЕФУцЛ§ЮЊ4ЃЛ
УыЪБЃЌЁїAPRЕФУцЛ§ЮЊ4ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуQзїQDЁЭACгкDЃЌ
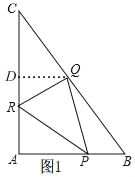
дкRtЁїABCжаЃЌABЃН6ЃЌACЃН8ЃЌИљОнЙДЙЩЖЈРэЕУЃЌBCЃН10ЃЌ
ЁрsinCЃН![]() ЃЌ
ЃЌ
гЩдЫЖЏжЊЃЌBQЃН5tЃЌCRЃН4tЃЌ
ЁрCQЃНBCЉBQЃН10Љ5tЃЌ
ЁрдкRtЁїCDQжаЃЌQDЃНCQsinCЃН![]() ЃЈ10Љ5tЃЉЃН6Љ3tЃЌ
ЃЈ10Љ5tЃЉЃН6Љ3tЃЌ
ЁрSЁїCQRЃН![]() CRQDЃН
CRQDЃН![]() ЁС4tЁСЃЈ6Љ3tЃЉЃН12tЉ6t2ЃНЉ6ЃЈtЉ1ЃЉ2+6ЃЌ
ЁС4tЁСЃЈ6Љ3tЃЉЃН12tЉ6t2ЃНЉ6ЃЈtЉ1ЃЉ2+6ЃЌ
Ёп0ЁмtЁм2ЃЌ
ЁрЕБtЃН1ЪБЃЌSЁїCQRзюДѓЃН6ЃЛ
ЃЈ3ЃЉДцдкЃЌШчЭМ2ЃЌЙ§ЕуRзїREЁЭBCгкEЃЌЙ§ЕуPзїPFЁЭBCгкFЃЌ
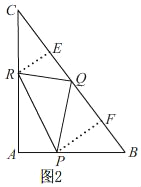
гЩЬтвтжЊЃЌCRЃН4tЃЌBQЃН5tЃЌAPЃН3tЃЌ
ЁрBPЃН6Љ3tЃЌ
ЁпЁЯBFPЃНЁЯAЃН90ЁуЃЌЁЯBЃНЁЯBЃЌ
ЁрЁїBFPЁзЁїBACЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрFPЃН![]() ЃЈ6Љ3tЃЉЃЌBFЃН
ЃЈ6Љ3tЃЉЃЌBFЃН![]() ЃЈ6Љ3tЃЉЃЌ
ЃЈ6Љ3tЃЉЃЌ
ЁрFQЃНBQЉBFЃН5tЉ![]() ЃЈ6Љ3tЃЉЃН
ЃЈ6Љ3tЃЉЃН![]()
ЭЌРэЃКEQЃН![]() ЃЌREЃН
ЃЌREЃН![]() ЃЌ
ЃЌ
ЁпЁЯREQЃНЁЯQFPЃН90ЁуЃЌ
ЁрЁЯERQ+ЁЯEQRЃН90ЁуЃЌ
ЁпЁЯPQRЃН90ЁуЃЌ
ЁрЁЯEQR+ЁЯPQFЃН90ЁуЃЌ
ЁрЁЯERQЃНЁЯPQFЃЌ
ЁрЁїREQЁзЁїQFPЃЎ
Ёр![]() ЃЌ
ЃЌ
ЁрREЁСFPЃНQFЁСEQЃЌ
Ёр![]() ЁС
ЁС![]() ЃЈ6Љ3tЃЉЃН
ЃЈ6Љ3tЃЉЃН![]() ЁС
ЁС![]() ЃЌ
ЃЌ
НтЕУЃЌtЃН1ЛђtЃН![]()
ЁрtЕФжЕЮЊ1УыЛђ![]() УыЃЎ
УыЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() ЕФжБОЖ
ЕФжБОЖ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() бгГЄЯпЩЯЕФвЛЕуЃЌЙ§
бгГЄЯпЩЯЕФвЛЕуЃЌЙ§![]() Еузї
Еузї![]() ЕФЧаЯпЃЌЧаЕуЮЊ
ЕФЧаЯпЃЌЧаЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.

ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯдЫЖЏЃЌ
ЕФбгГЄЯпЩЯдЫЖЏЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌФуШЯЮЊ
ЃЌФуШЯЮЊ![]() ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЛЏЃЌЧѓГі
ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЛЏЃЌЧѓГі![]() ЕФДѓаЁ.
ЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
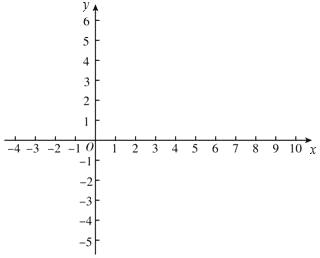
ЁОЬтФПЁПЫГДЮСЌНгЦНУцжБНЧзјБъЯЕxOyжаЃЌШЮвтЕФШ§ИіЕуPЃЌQЃЌGЃЎШчЙћЁЯPQGЃН90ЁуЃЌФЧУДГЦЁЯPQGЮЊЁАЛЦН№НЧЁБЃЎ
вбжЊЃКЕуAЃЈ0ЃЌ3ЃЉЃЌBЃЈ2ЃЌ3ЃЉЃЌCЃЈ3ЃЌ4ЃЉЃЌDЃЈ4ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉдкAЃЌBЃЌCЃЌDЫФИіЕужаФмЙЛЮЇГЩЁАЛЦН№НЧЁБЕФЕуЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌжБЯпyЃНkx+3ЃЈkЁй0ЃЉгывдOPЮЊжБОЖЕФдВНЛгкЕуQЃЈЕуQгыЕуOЃЌPВЛжиКЯЃЉЃЌЕБЁЯOQPЪЧЁАЛЦН№НЧЁБЪБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЪБЃЌжБЯпyЃНkx+3ЃЈkЁй0ЃЉгывдOPЮЊжБОЖЕФдВНЛгкЕуQЃЈЕуQгыЕуOЃЌPВЛжиКЯЃЉЃЌЕБЁЯOQPЪЧЁАЛЦН№НЧЁБЪБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБPЃЈtЃЌ0ЃЉЪБЃЌвдOPЮЊжБОЖЕФдВгыЁїBCDЕФШЮвЛБпНЛгкЕуQЃЌЕБЁЯOQPЪЧЁАЛЦН№НЧЁБЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊxЃН1ЃЌгыyжсЕФНЛЕуBдкЃЈ0ЃЌ2ЃЉКЭЃЈ0ЃЌ3ЃЉжЎМфЃЈАќКЌетСНИіЕуЃЉдЫЖЏЃЎгаШчЯТЫФИіНсТлЃКЂйХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈ3ЃЌ0ЃЉЃЛЂкЕуCЃЈx1ЃЌy1ЃЉЃЌDЃЈx2ЃЌy2ЃЉдкХзЮяЯпЩЯЃЌЧвТњзуx1ЃМx2ЃМ1ЃЌдђy1ЃОy2ЃЛЂлГЃЪ§ЯюcЕФШЁжЕЗЖЮЇЪЧ2ЁмcЁм3ЃЛЂмЯЕЪ§aЕФШЁжЕЗЖЮЇЪЧЉ1ЁмaЁмЉ![]() ЃЎЩЯЪіНсТлжаЃЌЫљгае§ШЗНсТлЕФађКХЪЧЃЈЁЁЁЁЃЉ
ЃЎЩЯЪіНсТлжаЃЌЫљгае§ШЗНсТлЕФађКХЪЧЃЈЁЁЁЁЃЉ
A. ЂйЂкЂл B. ЂкЂлЂм C. ЂйЂм D. ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
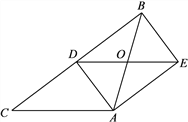
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌADЪЧBCБпЕФжаЯпЃЌЙ§ЕуAзїBCЕФЦНааЯпЃЌЙ§ЕуBзїADЕФЦНааЯпЃЌСНЯпНЛгкЕуE.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮADBEЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНгDEЃЌНЛABгкЕуOЃЌШєBC=8ЃЌAO=![]() ЃЌЧѓcosЁЯAEDЕФжЕ.
ЃЌЧѓcosЁЯAEDЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
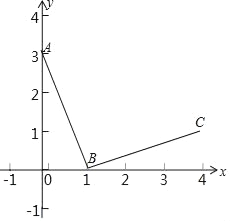
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЃЈ0ЃЌ3ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌСЌНгBAЃЌНЋЯпЖЮBAШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮBCЃЌЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓGОЙ§ЕуCЃЎ
ЕФЭМЯѓGОЙ§ЕуCЃЎ
ЃЈ1ЃЉЧыжБНгаДГіЕуCЕФзјБъМАkЕФжЕЃЛ
ЃЈ2ЃЉШєЕуPдкЭМЯѓGЩЯЃЌЧвЁЯPOBЃНЁЯBAOЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєQЃЈ0ЃЌmЃЉЮЊyжсе§АыжсЩЯвЛЕуЃЌЙ§ЕуQзїxжсЕФЦНааЯпгыЭМЯѓGНЛгкЕуMЃЌгыжБЯпOPНЛгкЕуNЃЌШєЕуMдкЕуNзѓВрЃЌНсКЯЭМЯѓЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯACBЃН90ЁуЃЌOCЃН2BOЃЌACЃН6ЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§AЁЂBСНЕуЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕуPЪЧжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїPDДЙжБxжсгкЕуDЃЌНЛЯпЖЮABгкЕуEЃЌЪЙPEЃН![]() DEЃЎ
DEЃЎ
ЂйЧѓЕуPЕФзјБъЃЛ
ЂкдкжБЯпPDЩЯЪЧЗёДцдкЕуMЃЌЪЙЁїABMЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЗћКЯЬѕМўЕФЫљгаЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
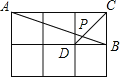
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФаЁе§ЗНаЮЭјИёжаЃЌЕуAЁЂBЁЂCЁЂDЖМдкетаЉаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌСЌНсCDгыABЯрНЛгкЕуPЃЌдђtanЁЯAPDЕФжЕЪЧ( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
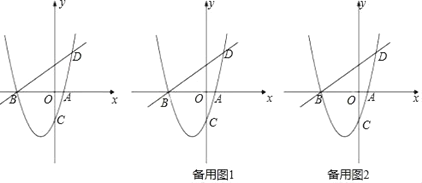
ЁОЬтФПЁП(12Зж)ШчЭМЃЌвбжЊХзЮяЯпyЃНax2+bxЉ2(aЁй0)гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌжБЯпBDНЛХзЮяЯпгкЕуDЃЌВЂЧвD(2ЃЌ3)ЃЌB(Љ4ЃЌ0)ЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)вбжЊЕуMЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌЧвдкЕкШ§ЯѓЯоЃЌЫГДЮСЌНгЕуBЁЂMЁЂCЃЌЧѓЁїBMCУцЛ§ЕФзюДѓжЕЃЛ
(3)дк(2)жаЁїBMCУцЛ§зюДѓЕФЬѕМўЯТЃЌЙ§ЕуMзїжБЯпЦНаагкyжсЃЌдкетЬѕжБЯпЩЯЪЧЗёДцдквЛИівдQЕуЮЊдВаФЃЌOQЮЊАыОЖЧвгыжБЯпACЯрЧаЕФдВЃПШєДцдкЃЌЧѓГідВаФQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com