
【题目】顺次连接平面直角坐标系xOy中,任意的三个点P,Q,G.如果∠PQG=90°,那么称∠PQG为“黄金角”.
已知:点A(0,3),B(2,3),C(3,4),D(4,3).
(1)在A,B,C,D四个点中能够围成“黄金角”的点是 ;
(2)当![]() 时,直线y=kx+3(k≠0)与以OP为直径的圆交于点Q(点Q与点O,P不重合),当∠OQP是“黄金角”时,求k的取值范围;
时,直线y=kx+3(k≠0)与以OP为直径的圆交于点Q(点Q与点O,P不重合),当∠OQP是“黄金角”时,求k的取值范围;
(3)当P(t,0)时,以OP为直径的圆与△BCD的任一边交于点Q,当∠OQP是“黄金角”时,求t的取值范围.
【答案】(1)B,C,D;(2)﹣![]() ≤k<0;(3)6≤t≤
≤k<0;(3)6≤t≤![]() .
.
【解析】
(1)描点,顺次连接,看有几个90°角.
(2)根据直线与圆有交点,分为相切和相交两种情况进行求解.当相切时,根据切线的性质及J(![]() ,0),F(0,3)求出∠JFO=∠JFQ=30°,从而求∠OFH=60°,最终求的H点的坐标代入直线方程即可.当相交时都符合条件,最终求出k的范围
,0),F(0,3)求出∠JFO=∠JFQ=30°,从而求∠OFH=60°,最终求的H点的坐标代入直线方程即可.当相交时都符合条件,最终求出k的范围
(3)根据(2)的分析,找出圆与三角形相切或相交的两种极限情况求出的值,即为t边界情况.
解:(1)观察图象可知:∠BCD=90°,
∴在A,B,C,D四个点中能够围成“黄金角”的点是B,C,D;
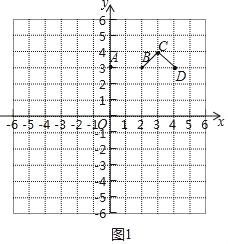
故答案为B,C,D.
(2)如图2中,当直线y=kx+3与⊙J相切时,设直线y=kx+3交y轴于点F,交x轴于点H,切点为Q,连接FJ.
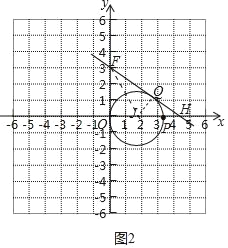
∵FO,FQ是切线,
∴∠JFO=∠JFQ,
∵J(![]() ,0),F(0,3),
,0),F(0,3),
∴tan∠JFO=![]()
∴∠JFO=∠JFQ=30°,
∴∠OFH=60°,
∴OH=![]() OF=3
OF=3![]() ,
,
∴H(3![]() ,0),
,0),
把H(3![]() ,0)代入y=kx+3,
,0)代入y=kx+3,
得到k=﹣![]() ,
,
观察图象可知:当直线y=kx+3与⊙j有交点时,∠OQP是“黄金角”(点Q与点O,P不重合),
∴﹣![]() ≤k<0.
≤k<0.
(3)如图3中,设以OP为直径的圆的圆心为J.
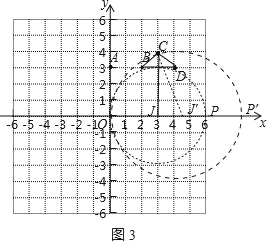
由题意可知当以OP为直径的圆与△BCD的边有交点时,∠OQP是“黄金角”,
当⊙J与△BCD的边相切时,J(3,0).此时P(6,0),t=6.
当⊙J′经过等C时,连接CJ′,CJ.设OJ′=CJ′=r,
在Rt△CJJ′中,r2=(r﹣3)2+42,
解得r=![]() ,
,
∴OP′=![]() ,
,
∴P′(![]() ,0),
,0),
观察图象可知:当6≤t≤![]() 时,∠OQP是“黄金角”.
时,∠OQP是“黄金角”.


科目:初中数学 来源: 题型:
【题目】如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
(1)求∠ACM的度数;
(2)在MN上是否存在一点D,使ABCD=ACBC,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体(如图),现已画出了主视图与俯视图.
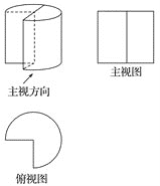
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只须保留作图痕迹);
(2)若此零件底面圆的半径r=2cm,高h=3cm,求此零件的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是多少?
(3)若该校九年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
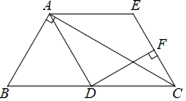
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,连OC,求∠BOC的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
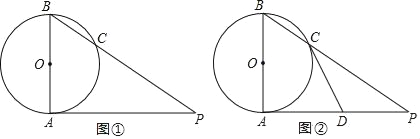
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P、Q、R分别在AB、BC、CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,用t(秒)(0≤t≤2)表示运动时间,在运动过程中:
(1)当t为何值时,△APR的面积为4;
(2)求出△CRQ的最大面积;
(3)是否存在t,使∠PQR=90°?若存在,请求出t的值;若不存在,请说明理由.
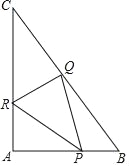
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com