
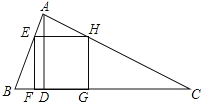
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
【答案】(1)证明见解析;(2)边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
【解析】
试题分析:(1)根据EH∥BC即可证明.
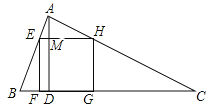
(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
试题解析:(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,∴正方形EFGH的边长为
,∴正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= ![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有(填序号).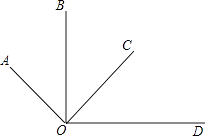
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车队运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,不仅装完全部货物,并且其中有一辆车只装了3.5吨。这个汽车队共派了多少辆汽车运输这批货物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com