
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( ) 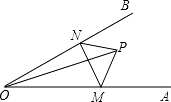
A.25°
B.30°
C.35°
D.40°
【答案】B
【解析】解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB= ![]() ∠COD,
∠COD,
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
故选:B.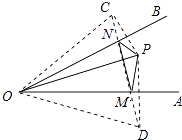
【考点精析】本题主要考查了轴对称-最短路线问题的相关知识点,需要掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】要得到y=(x﹣3)2﹣2的图象,只要将y=x2的图象( )
A.由向左平移3个单位,再向上平移2个单位
B.由向右平移3个单位,再向下平移2个单位
C.由向右平移3个单位,再向上平移2个单位
D.由向左平移3个单位,再向下平移2个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
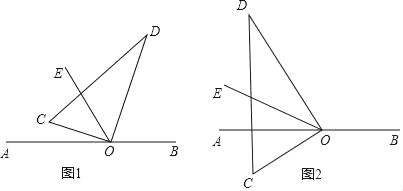
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
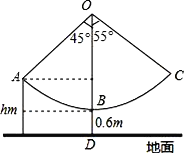
【题目】枣庄乐园设置了一个秋千场所,如图所,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,求h的长;
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
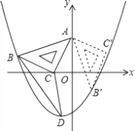
【题目】如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的关系式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)将三角板ABC绕顶点A逆时针方向旋转90°,到达△AB′C的位置.请判断点B′C′是否在(2)中的抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10cm,OC=6cm.F是线段OA上的动点,从点O出发,以1cm/s的速度沿OA方向作匀速运动,点Q在线段AB上.已知A,Q两点间的距离是O,F两点间距离的a倍.若用(a,t)表示经过时间t(s)时,△OCF,△FAQ,△CBQ中有两个三角形全等.请写出(a,t)的所有可能情况 . 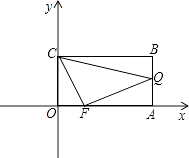
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( ) 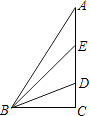
A.BC是△ABE的高
B.BE是△ABD的中线
C.BD是△EBC的角平分线
D.∠ABE=∠EBD=∠DBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com