
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

【答案】(1)见解析 (2)见解析 (3)![]() m°
m°
【解析】分析:(1)如图1中,欲证明BD=EC,只要证明△DAB≌△EAC即可;
(2)如图2中,延长DC到E,使得DB=DE.首先证明△BDE是等边三角形,再证明△ABD≌△CBE即可解决问题;
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.想办法证明△AFE≌△AFG,可得∠EAF=∠FAG=![]() m°.
m°.
详(1)证明:如图1中,
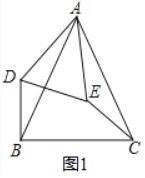
∵∠BAC=∠DAE,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
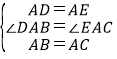 ,
,
∴△DAB≌△EAC,
∴BD=EC.
(2)证明:如图2中,延长DC到E,使得DB=DE.
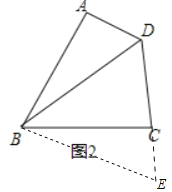
∵DB=DE,∠BDC=60°,
∴△BDE是等边三角形,
∴∠BD=BE,∠DBE=∠ABC=60°,
∴∠ABD=∠CBE,
∵AB=BC,
∴△ABD≌△CBE,
∴AD=EC,
∴BD=DE=DC+CE=DC+AD.
∴AD+CD=BD.
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.
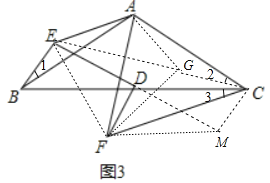
由(1)可知△EAB≌△GAC,
∴∠1=∠2,BE=CG,
∵BD=DC,∠BDE=∠CDM,DE=DM,
∴△EDB≌△MDC,
∴EM=CM=CG,∠EBC=∠MCD,
∵∠EBC=∠ACF,
∴∠MCD=∠ACF,
∴∠FCM=∠ACB=∠ABC,
∴∠1=3=∠2,
∴∠FCG=∠ACB=∠MCF,
∵CF=CF,CG=CM,
∴△CFG≌△CFM,
∴FG=FM,
∵ED=DM,DF⊥EM,
∴FE=FM=FG,
∵AE=AG,AF=AF,
∴△AFE≌△AFG,
∴∠EAF=∠FAG=![]() m°.
m°.


科目:初中数学 来源: 题型:
【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水—清冼—灌水”的过程.某游泳馆从早上7:00开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的1.6倍,其中游泳池内剩余的水量y(m3)与换水时间x(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)填空:该游泳池清洗需要 小时;
(2)求排水过程中的y(m3)与x(h)之间的函数关系式,并写出自变量x的取值范围;
(3)若该游泳馆在换水结束后30分钟才能对外开放,试问游泳爱好者小明能否在中午12:40进入该游泳馆游泳?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别![]() a、
a、![]() a、
a、![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若![]() ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
①<1.493>=1;
②<2x>=2<x>;
③若![]() ,则实数x的取值范围是
,则实数x的取值范围是![]() ;
;
④当x≥0,m为非负整数时,有![]() ;
;
⑤![]() 。
。
其中,正确的结论有 (填写所有正确的序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A点测得顶端D的仰角∠DAC=30°,向前走了46米到达B点后,在B点测得顶端D的仰角∠DBC=45°.求永定楼的高度CD.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
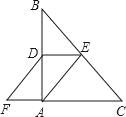
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com