
【题目】如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
【答案】
(1)证明:连接OD,
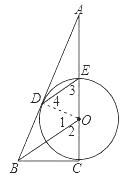
∵DE∥BO,
∴∠1=∠4,∠2=∠3,
∵OD=OE,
∴∠3=∠4,
∴∠1=∠2,
在△DOB与△COB中,
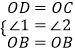 ,
,
∴△DOB≌△COB,
∴∠OCB=∠ODB,
∵BD切⊙O于点D,
∴∠ODB=90°,
∴∠OCB=90°,
∴AC⊥BC,
∴直线BC是⊙O的切线
(2)解:∵∠DEO=∠2,
∴tan∠DEO=tan∠2= ![]() ,
,
设OC=r,BC= ![]() r,
r,
由(1)证得△DOB≌△COB,
∴BD=BC= ![]() r,
r,
由切割线定理得:AD2=AEAC=2(2+r),
∴AD=2 ![]() ,
,
∵DE∥BO,
∴ ![]() ,
,
∴ ![]() ,
,
∴r=1,
∴AO=3.
【解析】(1)要证明直线BC是⊙O的切线,连接OD,根据已知先证明∠1=∠2,再证明△DOB≌△COB,得出∠OCB=∠ODB,然后根据切线的性质证明∠OCB=90°,即可证得结论。
(2)利用tan∠DEO= ![]() ,得出 tan∠2=
,得出 tan∠2= ![]() ,由△DOB≌△COB得出BD=BC,再根据切割线定理,证得AD2=AEAC,可表示出AD的长,再由DE∥BO,得对应线段成比例,求出r的长,即可求出AO的长。
,由△DOB≌△COB得出BD=BC,再根据切割线定理,证得AD2=AEAC,可表示出AD的长,再由DE∥BO,得对应线段成比例,求出r的长,即可求出AO的长。
【考点精析】利用平行线分线段成比例和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知三条平行线截两条直线,所得的对应线段成比例;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ![]() ,AF=4
,AF=4 ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,且当x=0时,y=﹣4;且图象通过点(1,﹣2)
(1)求这个一次函数的解析式;
(2)判断点(a,2a﹣4)是否在该函数图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学课上,老师要求学生根据图示张鑫与李亮的对话内容,展开如下活动:
活动1:仔细阅读对话内容

活动2:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,她需要付多少钱?
(2)你认为买多少元钱的书办卡就便宜?
查看答案和解析>>
科目:初中数学 来源: 题型:
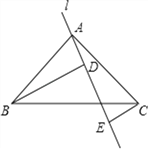
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com