
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
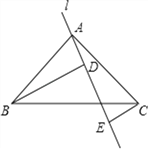
【答案】(1)AD与CE的大小关系为AD=CE,理由见解析;
(2)线段BD,DE,CE之间的数量之间关系为:BD=DE+CE,理由见解析.
【解析】试题分析:(1)由已知可得AB=AC,∠BDA=∠AEC=90°,∠BAD=∠ACE;两角及其一角的对边对应相等的两个三角形全等,利用△ABD≌△CAE即可得到AD=CE;(2)据△ABD≌△CAE,可得BD=AE,AD=EC,又AE=AD+DE,故可得BD=DE+CE.
试题解析:(1)AD与CE的大小关系为AD=CE,
理由是:∵∠BAD+∠EAC=∠BAC=90°,
又∵CE⊥l于E,
∴∠ACE+∠EAC=90°,
∴∠BAD=∠ACE;
∵BD⊥l于D,CE⊥l于E,
∴∠BDA=∠AEC=90°;
又∵AB=AC;
∴△ABD≌△CAE(AAS),
∴AD=CE.
(2)线段BD,DE,CE之间的数量之间关系为:BD=DE+CE,理由如下:
∵△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=DE+AD,
∴BD=DE+CE.


科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
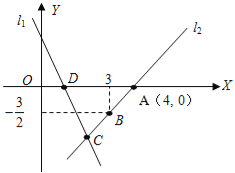
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校调查了20名男生某一周参加篮球运动的次数,调查结果如下表所示,那么这20名男生在该周参加篮球运动次数的平均数是( )
次数 | 2 | 3 | 4 | 5 |
人数 | 2 | 2 | 10 | 6 |
A. 3B. 3.5C. 4D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动。规定当其中一个动点到达端点时,另一个动点也随之停止运动。设运动时间为t,求:
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在电影院内,如果将“12排8号”记作(12,8),那么“5排9号”怎样表示?(23,15)表示的含义是什么?( )
A. (9,5);23排15号 B. (5,9);23排15号
C. (9,5);15排23号 D. (5,9);15排23号
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com