
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动。规定当其中一个动点到达端点时,另一个动点也随之停止运动。设运动时间为t,求:
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?

【答案】(1)当t=6时,PQ∥CD;
(2)当t=6或t=7时,PQ=CD.
【解析】试题分析:(1)由当PQ∥CD时,四边形PQCD为平行四边形,可得方程24-t=3t,解此方程即可求得答案;
(2)根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24-t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t-(24-t)=4时,四边形PQCD为等腰梯形,解此方程即可求得答案.
试题解析:根据题意得:PA=t,CQ=3t,则PD=AD-PA=24-t.
(1)∵AD∥BC,
即PQ∥CD,
∴当PD=CQ时,四边形PQCD为平行四边形,
即24-t=3t,
解得:t=6,
即当t=6时,PQ∥CD;
(2)若PQ=DC,分两种情况:
①PQ=DC,由(1)可知,t=6,
②PQ≠DC,由QC=PD+2(BC-AD),
可得方程:3t=24-t+4,
解得:t=7.


科目:初中数学 来源: 题型:
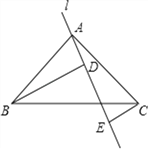
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
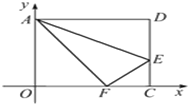
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. “买一张彩票中大奖”是随机事件
B. 不可能事件和必然事件都是确定事件
C. “穿十条马路连遇十次红灯”是不可能事件
D. “太阳东升西落”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
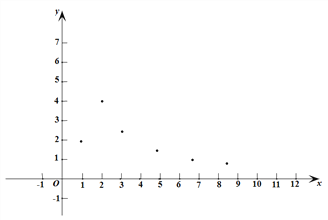
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
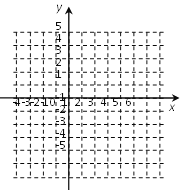
【题目】在平面直角坐标系中,O为坐标原点,已知A(0,a),B(b,b),C(c,a),其中a,b满足关系式|a-4|+ (b-2)2=0,c=a+b.
(1)求A、B、C三点的坐标,并在坐标系中画出△ABC;
(2)如果在第四象限内有一点P(2,m),请用含m的代数式表示三角形CPO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com