
【题目】按照下列要求画图并填空:
(1)过点![]() 画出直线
画出直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ,那么点
,那么点![]() 到直线
到直线![]() 的距离是线段______________的长.
的距离是线段______________的长.
(2)作出△![]() 的边
的边![]() 的垂直平分线
的垂直平分线![]() ,分别交边
,分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,联结
,联结![]() ,那么线段
,那么线段![]() 是△
是△![]() 的______________.(保留作图痕迹)
的______________.(保留作图痕迹)

【答案】答案见解析
【解析】分析:(1)以点B为圆心,以任意长为半径画弧,与AC的延长线相交于两点,在以这两点为圆心,以大于它们距离的一半为半径画弧,两弧相交于一点,连接点B与这一点与AC的延长线相交于点D,则点D即为所求,根据点到直线的距离解答;
(2)分别以点A、B为圆心,以大于![]() AB为半径画弧,两弧相交于两点,过这两点作直线EF即可,根据线段垂直平分线的定义可得点M是AB的中点,然后根据中线的定义解答.
AB为半径画弧,两弧相交于两点,过这两点作直线EF即可,根据线段垂直平分线的定义可得点M是AB的中点,然后根据中线的定义解答.
详解:(1)如图所示,BD为所求作的垂线,点B到直线AC的距离是线段BD的长度,
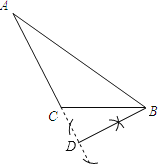
故答案为:BD;
(2)如图所示,EF为所求作的线段AB的垂直平分线,
线段CM是△ABC的边AB的中线,
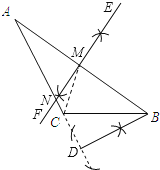
故答案为:边AB的中线.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(x,y),若点Q的坐标为(x+ay,ax+y)(其中a为常数,且a≠0),则称Q是点P的“a系联动点”.例如:点P(1,2)的“3系联动点”Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“![]() 系联动点”的坐标是(
系联动点”的坐标是(![]() ,0),则点P的坐标为 ;
,0),则点P的坐标为 ;
(2)若点P(x,y)的“a系联动点”与“![]() 系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
(3)在(2)的条件下,点P不与原点重合,点P的“a系联动点”为点Q,且PQ的长度为OP长度的3倍,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2m+1)x+m2+m=0.
(1)求证:方程恒有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,且满足![]() =13,求实数m的值.
=13,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品批发商场共用22000元同时购进A、B两种型号背包各400个,购进A型号背包30个比购进B型背包15个多用300元.
(1)求A、B两种型号背包的进货单价各为多少元?
(2)若商场把A、B两种型号背包均按每个50元定价进行零售,同时为扩大销售,拿出一部分背包按零售价的7折进行批发销售.商场在这批背包全部售完后,若总获利超过10500元,则商场用于批发的背包数量最多为多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 在边
在边![]() 的延长线上,
的延长线上,![]() 平分
平分![]() ,说明
,说明![]() ∥
∥![]() 的理由.
的理由.

解:因为点![]() 在边
在边![]() 的延长线上(已知),
的延长线上(已知),
所以![]() (______________________).
(______________________).
因为![]() (已知),
(已知),
所以![]() (等式性质).
(等式性质).
因为![]() 平分
平分![]() (已知),
(已知),
所以![]() (___________________).
(___________________).
因为![]() (_________________________________),
(_________________________________),
所以![]() (等量代换).
(等量代换).
所以![]() ∥
∥![]() (____________________________________).
(____________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
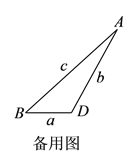
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com