
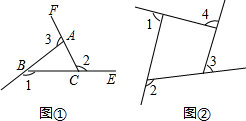
 (1)图①中,射线AD,BE,CF构成∠1,∠2,∠3,量出∠1,∠2,∠3,并计算∠1+∠2+∠3.画出几个类似的图,计算相应的三个角的和,你有什么发现?
(1)图①中,射线AD,BE,CF构成∠1,∠2,∠3,量出∠1,∠2,∠3,并计算∠1+∠2+∠3.画出几个类似的图,计算相应的三个角的和,你有什么发现?科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.| 2n |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市八士中学七年级上学期期末考试数学试卷(带解析) 题型:解答题
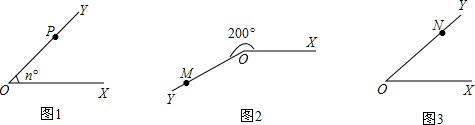
如图1,将射线OX绕点O按逆时针旋转n°的角,得到射线OY,如果点P为射线OY上一点,且OP=a,那么我们就规定用(a,n°)表示点P在平面内的位置,并记为P(a,n°).例如在图2中,如果OM=6,∠XOM=200°,那么点M在平面内的位置记为M(6,200°). 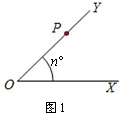
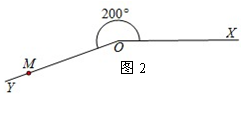
根据上述规定解答下列问题:
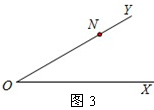
(1)在图3中,如果点N在平面内的位置记为N(10,35°),那么ON=____,∠XON=____°;
(2)将图3中的射线OY绕点O旋转一定的角度(小于360度),使得旋转后所得到的射线OZ与射线OY垂直,则旋转后点N在平面内的位置可记为_______ _,请在图3中画出旋转后的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com