
解:(1)如图,∵在△ABC中,AB=AC=2,∠A=90°,
∴∠B=∠C=45°.
又∵∠1=180°-∠EPF-∠3,∠EPF=45°,∠C+∠2+∠3=180°,
∴∠1=135°-∠3,∠2=135°-∠3,
∴∠2=∠3,
∴△BPE∽△CFP.
(2)如图,∵在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,
∴BP=CP=

.
由(1)知△BPE∽△CFP,则
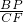
=
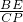
,即

=
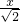
,
解得,CF=

.
则S
△PEF=S
△ABC-S
△BPE-S
△PFC-S
△AEF=

×2×2-

×

x×sinB-

×

×

×sinC-

×(2-x)×(2-

)
=2-

×

x×

-

×

×

×

-

×(2-x)×(2-

)
=-1+

+

,即y=-1+

+

(1≤x≤2);
(3)当E、F在运动过程中,∠EFP可能等于60°.理由如下:
假设当E、F在运动过程中,∠EFP是等于60°.
如图,过点E作EM⊥FP于点M.
设FM=a.
在Rt△EMF中,EM=

a.
在Rt△EMP中,得到PM=

a,EP=

a,
则

=

=

,
∵△BPE∽△CFP,
∴
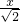
=

,
∴x=3-

.
∵1≤x≤2,
∴x=3-

符合题意,
∴当E、F在运动过程中,∠EFP可能等于60°.
分析:(1)由等腰直角三角形的性质求得∠B=∠C=45°;然后由三角形内角和定理、邻补角的定义求得∠BPE=∠CFP,则由“两角法”证得结论;
(2)S
△PEF=S
△ABC-S
△BPE-S
△PFC-S
△AEF;
(3)利用反证法证明.假设当E、F在运动过程中,∠EFP是等于60°.如图,过点E作EM⊥FP于点M.设FM=a.构造两个直角三角形,通过解图中的两个直角三角形分别求得EM=

a.PM=

a,EP=

a,则

=

=

;再利用(1)中的全等三角形的对应边成比例得到
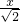
=

,解得x的值符合(2)中的取值范围时,假设成立.反之,假设不成立.
点评:本题考查了相似三角形的判定与性质、等腰直角三角形的性质.在利用相似三角形的对应边成比例来解题时,一定要找准“对应边”.

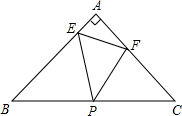 如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.
如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°. 解:(1)如图,∵在△ABC中,AB=AC=2,∠A=90°,
解:(1)如图,∵在△ABC中,AB=AC=2,∠A=90°, .
.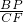 =
=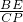 ,即
,即 =
=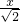 ,
, .
. ×2×2-
×2×2- ×
× x×sinB-
x×sinB- ×
× ×
× ×sinC-
×sinC- ×(2-x)×(2-
×(2-x)×(2- )
) ×
× x×
x× -
- ×
× ×
× ×
× -
- ×(2-x)×(2-
×(2-x)×(2- )
) +
+ ,即y=-1+
,即y=-1+ +
+ (1≤x≤2);
(1≤x≤2); a.
a. a,EP=
a,EP= a,
a, =
= =
= ,
,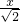 =
= ,
, .
. 符合题意,
符合题意, a.PM=
a.PM= a,EP=
a,EP= a,则
a,则 =
= =
= ;再利用(1)中的全等三角形的对应边成比例得到
;再利用(1)中的全等三角形的对应边成比例得到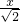 =
= ,解得x的值符合(2)中的取值范围时,假设成立.反之,假设不成立.
,解得x的值符合(2)中的取值范围时,假设成立.反之,假设不成立.

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为