
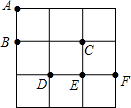
 ��3��3�ķ���ֽ�У���A��B��C��D��E��F�ֱ�λ����ͼ��ʾ��С�����εĶ����ϣ�
��3��3�ķ���ֽ�У���A��B��C��D��E��F�ֱ�λ����ͼ��ʾ��С�����εĶ����ϣ����� ��1�����������оٷ��ɵã���B��C��D��E��F�����������ȡ���㣬�ȿ��ܽ���У�BCD��BCE��BCF��BDE��BDF��BEF��CDE��CDF��CEF��DEF�����������������ǵ���ֱ�������ε��У���BCD����CDE����CEF����CDF����ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ���������ı�����ƽ���ı��ε������Ȼ�����ø��ʹ�ʽ��⼴����ô𰸣�
��� �⣺��1���ߴ�B��C��D��E��F�����������ȡ���㣬�ȿ��ܽ���У���BCD����BCE����BCF����BDE����BDF����BEF����CDE����CDF����CEF����DEF�����������������ǵ���ֱ�������ε��У���BCD����CDE����CEF����CDF��
���B��C��D��E��F�����������ȡ���㣬����ȡ��������Ϊ���㻭�����Σ��������������ǵ���ֱ�������εĸ����ǣ�$\frac{4}{10}$=$\frac{2}{5}$��
�ʴ�Ϊ��$\frac{2}{5}$��
��2������״ͼ�ã�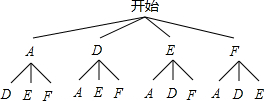
�߹���12�ֵȿ��ܵĽ���������ı�����ƽ���ı��ε���2�������
�������ı�����ƽ���ı��εĸ���Ϊ��$\frac{2}{12}$=$\frac{1}{6}$��
���� ���⿼������״ͼ�����б�������ʣ��õ���֪ʶ��Ϊ������=������������������֮�ȣ�


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
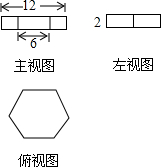 ��ͼ��ʾ��ij�����������ͼ����ü����������ǣ�������
��ͼ��ʾ��ij�����������ͼ����ü����������ǣ�������| A�� | 18$\sqrt{3}$ | B�� | 54$\sqrt{3}$ | C�� | 108$\sqrt{3}$ | D�� | 216$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | $\frac{1}{3}$ | D�� | -$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
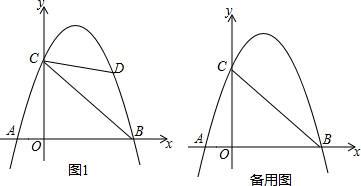
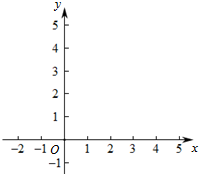 ��ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{4}{x^2}$+bx+c������A��4��0����B��0��2��
��ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{4}{x^2}$+bx+c������A��4��0����B��0��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
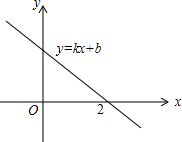 ��ͼ��һ�κ���y=kx+b��ͼ����x��Ľ���Ϊ��2��0����������˵����ȷ���Т٢ڢ�
��ͼ��һ�κ���y=kx+b��ͼ����x��Ľ���Ϊ��2��0����������˵����ȷ���Т٢ڢ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
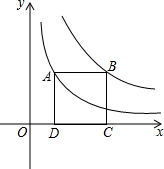 ��ͼ����A��˫����y=$\frac{2}{x}$�ϣ���B��˫����y=$\frac{6}{x}$�ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ�����Σ���AB=2��
��ͼ����A��˫����y=$\frac{2}{x}$�ϣ���B��˫����y=$\frac{6}{x}$�ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ�����Σ���AB=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
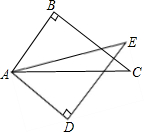 ��ͼ���ڡ�ABC�͡�ADE�У���B=��D=90�㣬AB=AD��Ҫʹ��ABC�ա�ADE��Ӧ����������C=��E��������һ���������ɣ�
��ͼ���ڡ�ABC�͡�ADE�У���B=��D=90�㣬AB=AD��Ҫʹ��ABC�ա�ADE��Ӧ����������C=��E��������һ���������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ�����������ֱ���ı��������� | |
| B�� | ��������ȵ��ı����������� | |
| C�� | �Խ������ֱ���ı�����ƽ���ı��� | |
| D�� | �Խ���������ƽ�ֵ��ı����Ǿ��� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com