
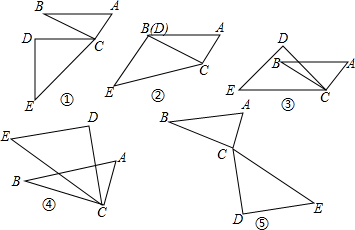
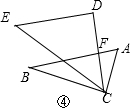
 ∴∠DCE=45°,
∴∠DCE=45°,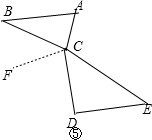 ∵∠B=30°,
∵∠B=30°,

 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
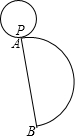 如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.
如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.查看答案和解析>>
科目:初中数学 来源: 题型:
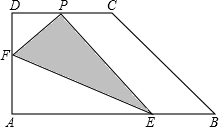 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于查看答案和解析>>
科目:初中数学 来源: 题型:
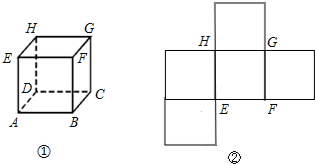
查看答案和解析>>
科目:初中数学 来源: 题型:
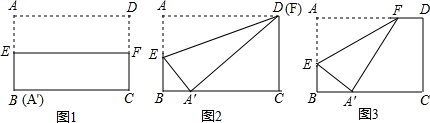
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com