
如图,等腰 中,
中, ,D是BC上一点,且
,D是BC上一点,且 .
.
(1)求证: ∽
∽ ;
;
(2)若 ,
, ,求BC的长;
,求BC的长;
(3)若 ,求
,求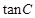 的值.
的值.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,垂足为D.
(1)若AD=9,BC=16,求BD的长;
(2)求证:AB2•BC=CD2•AD.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AB∥CD,∠DAB=90°,AC⊥BC.
(1)求证:△ADC∽△BCA;
(2)若AB=9cm,AC=6cm,求梯形ABCD中位线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠B= 90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动。
(1)如果P、Q分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?
(2)如果P、Q两分别从A、B两点同时出发,并且P到B又继续在BC边上前进,Q到C后又继续在CA边上前进,经过几秒钟,△PCQ的面积等于12﹒6厘米2 ?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
网格中每个小正方形的边长都是1.
(1)将图1中画一个格点三角形DEF,使得△DEF≌△ABC
(2)将图2中画一个格点三角形MNL,使得△MNL∽△ABC,且相似比为2:1
(3)将图3中画一个格点三角形OPQ,使得△OPQ∽△ABC,且相似比为 :1
:1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,在⊙O中,直径AB⊥CD于点E,连接BC.
(1)线段BC、BE、AB应满足的数量关系是 ;
(2)若点P是优弧 上一点(不与点C、A、D重合),连接BP与CD交于点G.
上一点(不与点C、A、D重合),连接BP与CD交于点G.
请完成下面四个任务:
①根据已知画出完整图形,并标出相应字母;
②在正确完成①的基础上,猜想线段BC、BG、BP应满足的数量关系是 ;
③证明你在②中的猜想是正确的;
④点P′恰恰是你选择的点P关于直径AB的对称点,那么按照要求画出图形后在②中的猜想仍然正确吗? ;(填正确或者不正确,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,矩形ABCD中,AB=21,AD=12,E是CD边上的一点,CE=5,M是BC边上的中点,动点P从点A出发,沿AB边以每秒1个单位长度的速度向终点B运动,连结PM.设动点P的运动时间是t秒.
(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.①当EP平分四边形PMEH的面积时,求t的值;②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com