
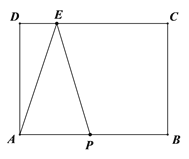
【题目】如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD边上的一点,且DE=2cm,动点P从A点出发,以2cm/s的速度沿A→B→C→E运动,最终到达点E.当△APE的面积等于20cm2时,求点P运动的时间.
【答案】当t=![]() s或6s时,△APE的面积等于20cm2.
s或6s时,△APE的面积等于20cm2.
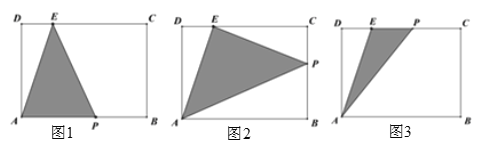
【解析】试题分析:分为三种情况讨论,如图1,当点P在AB上,即0<t≤4时,根据三角形的面积公式建立方程求出其解即可;如图2,当点P在BC上,即4<t≤7时,由S△APE=S四边形AECB-S△PCE-S△PAB建立方程求出其解即可;如图3,当点P在EC上,即7<t≤10时,由S△APE=![]() =20建立方程求出其解即可.
=20建立方程求出其解即可.
试题分析:设点P运动的时间为t s,
∵四边形ABCD是矩形,
∴AD=BC=6,AB=CD=8,
如图1,当点P在AB上,即0<t≤4时,此时AP=2t,S△APE=![]() ×2t×6=20,解得t=
×2t×6=20,解得t=![]() (s);
(s);
如图2,当点P在BC上,即4<t≤7时,此时BP=2t-8,CP=8+6-2t=14-2t,S△APE=48-S△ADE-S△ABP-S△PCE,
即20=48-![]() ×6×2-
×6×2-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×6×(14-2t),
×6×(14-2t),
解得:t=6(s);
如图3,当点P在EC上,即7<t≤10时,此时PE=8+6+8-2-2t=20-2t,S△APE=![]() =
=![]() ×6×(20-2t)=20,
×6×(20-2t)=20,
解得t=![]() (s),
(s),
∵![]() <7,∴t=
<7,∴t=![]() 应舍去;
应舍去;
综上所述,当t=![]() s或6s时,△APE的面积等于20cm2.
s或6s时,△APE的面积等于20cm2.


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
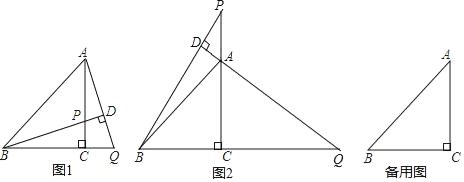
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.

(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家购进A、B两种商品,A种商品用了480元,B种商品用了1260元,A、B两种商品的数量比为1﹕3,A种商品每千克的进价比B种商品每千克的进价多2元.A、B两种商品各购进多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com