
����Ŀ�����꼶��3������ѧ��ȤС�龭���г�����������ij����Ʒ�ڵ�x�죨1��x��90����xΪ���������ۼ����������������Ϣ���£���֪��Ʒ�Ľ���Ϊ30Ԫ/���������Ʒ���ۼ�Ϊy����λ��Ԫ/������ÿ���������Ϊp����λ��������ÿ�����������Ϊw����λ��Ԫ����
ʱ��x���죩 | 1 | 30 | 60 | 90 |
ÿ��������p������ | 198 | 140 | 80 | 20 |

��1�����w��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ����������������������������
��3������Ʒ�����۹����У����ж�����ÿ�������������5600Ԫ����ֱ��д�������
���𰸡�
��1���⣺��0��x��50ʱ������Ʒ���ۼ�y��ʱ��x�ĺ�����ϵʽΪy=kx+b��k��bΪ������k��0����
��y=kx+b�����㣨0��40������50��90����
�� ![]() ����ã�
����ã� ![]() ��
��
���ۼ�y��ʱ��x�ĺ�����ϵʽΪy=x+40��
��50��x��90ʱ��y=90��
���ۼ�y��ʱ��x�ĺ�����ϵʽΪy= ![]() ��
��
����ǿ�֪ÿ���������p��ʱ��x��һ�κ�����ϵ��
��ÿ���������p��ʱ��x�ĺ�����ϵʽΪp=mx+n��m��nΪ��������m��0����
��p=mx+n���㣨60��80������30��140����
�� ![]() ����ã�
����ã� ![]() ��
��
��p=��2x+200��0��x��90����x��������
��0��x��50ʱ��w=��y��30��p=��x+40��30������2x+200��=��2x2+180x+2000��
��50��x��90ʱ��w=��90��30������2x+200��=��120x+12000��
������ʾ��ÿ�����������w��ʱ��x�ĺ�����ϵʽ��w= ![]()
��2���⣺��0��x��50ʱ��w=��2x2+180x+2000=��2��x��45��2+6050��
��a=��2��0��0��x��50��
�൱x=45ʱ��wȡ���ֵ�����ֵΪ6050Ԫ��
��50��x��90ʱ��w=��120x+12000��
��k=��120��0��w��x���������
�൱x=50ʱ��wȡ���ֵ�����ֵΪ6000Ԫ��
��6050��6000��
�൱x=45ʱ��w������ֵΪ6050Ԫ��
�����۵�45��ʱ�������õ���������������������6050Ԫ
��3���⣺��0��x��50ʱ����w=��2x2+180x+2000��5600������2x2+180x��3600��0��
��ã�30��x��50��
50��30+1=21���죩��
��50��x��90ʱ����w=��120x+12000��5600������120x+6400��0��
��ã�50��x��53 ![]() ��
��
��x������
��50��x��53��
53��50=3���죩��
���Ͽ�֪��21+3=24���죩��
�ʸ���Ʒ�����۹����У�����24��ÿ�������������5600Ԫ
����������1����0��x��50ʱ������Ʒ���ۼ�y��ʱ��x�ĺ�����ϵʽΪy=kx+b���ɵ���������ô���ϵ�������������ʱy����x�ĺ�����ϵʽ������ͼ�οɵó���50��x��90ʱ��y=90���ٽ�ϸ���������ÿ���������p��ʱ��x�ĺ�����ϵʽΪp=mx+n�������������ô���ϵ�����������p����x�ĺ�����ϵʽ��������������=��������������������ɵó�w����x�ĺ�����ϵʽ����2������w����x�ĺ�����ϵʽ���ֶο�������ֵ���⣮��0��x��50ʱ����϶��κ��������ʼ�������ڴ˷�Χ��w�����ֵ����50��x��90ʱ������һ�κ��������ʼ�������ڴ˷�Χ��w�����ֵ���������ֵ���Ƚϼ��ɵó����ۣ���3����w��5600���ɵó�����x��һԪ���β���ʽ��һԪһ�β���ʽ���ⲻ��ʽ���ɵó�x��ȡֵ��Χ���ɴ˼��ɵó����ۣ����⿼���˶��κ�����Ӧ�á�һԪһ�β���ʽ��Ӧ�á�һԪ���β���ʽ��Ӧ���Լ����ô���ϵ������������ʽ������Ĺؼ�����1�����ݵ���������ô���ϵ�������������ϵʽ����2�����ö��κ�����һ�κ��������ʽ����ֵ���⣻��3���ó�����x��һԪһ�κ�һԪ���β���ʽ�����������е��⣬�ѶȲ����Ϸ����������������Ŀʱ�����ݸ���������ϵ���ҳ�������ϵʽ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABCD�У�AB��CD����ABC=90�㣬AB=2BC=2CD���Խ���AC��BD�ཻ�ڵ�O���߶�OA��OB���е�ֱ�ΪE��F��
��1����֤����FOE�ա�DOC��
��2����sin��OEF��ֵ��
��3����ֱ��EF���߶�AD��BC�ֱ��ཻ�ڵ�G��H���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD=BC��AC=BD�� 
��1����֤����ADB�ա�BCA��
��2��OA��OB���������ȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ��ǡ�ABC�ı�AB��BC�ϵĵ㣬��DE��AC��AE��CD�ཻ�ڵ�O����S��DOE��S��COA=1��25����S��BDE��S��CDE�ı��ǣ������� 
A.1��3
B.1��4
C.1��5
D.1��25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧΪ�����������������ȫУϲ��ƹ����������ë�������������������˶���1000��ѧ���У������ȡ��������ѧ�����е��飬�˽�ѧ����ϲ����һ�������˶���ÿ��ֻ���������������˶���ѡ��һ�֣�������ͳ�����£�
�������� | ƹ���� | ���� | ��ë�� | ���� | ���� |
���� | a | 12 | 36 | 18 | b |

����������⣺
��1�����ε����е�������������
��2��a= �� b=��
��3���Թ�������1000��ѧ������ϲ����ë���˶���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O����BAC=120�㣬AB=AC��BDΪ��O��ֱ����AD=6����DC= �� 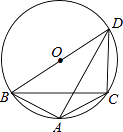
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��E��AB���е㣬����DE���ӳ���CB���ӳ����ڵ�F����G�ڱ�BC�ϣ��ҡ�GDF=��ADF�� 
��1����֤����ADE�ա�BFE��
��2������EG���ж�EG��DF��λ�ù�ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬����˵���в���ȷ���ǣ�������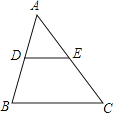
A.DE= ![]() BC
BC
B.![]()
C.��ADE�ס�ABC
D.S��ADE��S��ABC=1��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com